
【题目】(2015·湖南)设![]() ,且
,且![]() ,证明
,证明
(1)![]()
(2)![]() 与
与![]() 不可能同时成立
不可能同时成立
【答案】
(1)
由a>0,b>0,
则![]() ,
,
由于![]() ,则
,则![]() ,
,
即有![]() ,
,
当且仅当![]() 取得等号,
取得等号,
则![]()
(2)
假设![]() 与
与![]() 同时成立,
同时成立,
由![]() 及
及![]() 可得
可得![]()
由![]() 及
及![]() 可得
可得![]()
这与![]() 矛盾
矛盾
所以![]() 与
与![]() 不可能同时成立
不可能同时成立
【解析】(1)将已知条件中的式子可等价变形为,再由基本不等式即可得证详见解答(1)(2)利用反证发,假设与同时成立,可求得,从而与矛盾,即可得证,详见解答(2)
本题主要考查了不等式的证明与反证法等知识点,属于中档题,第一小问需将条件中的式子作等价变形,再利用基本不等式即可求解,第二小问从问题不可能同时成立,可以考虑采用反证法证明,否定结论,从而推出矛盾,反证法作为一个相对冷门的数学方法,在后续复习时亦应予以关注.
【考点精析】根据题目的已知条件,利用基本不等式和反证法的相关知识可以得到问题的答案,需要掌握基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() ;从命题结论的反面出发(假设),引出(与已知、公理、定理…)矛盾,从而否定假设证明原命题成立,这样的证明方法叫做反证法.
;从命题结论的反面出发(假设),引出(与已知、公理、定理…)矛盾,从而否定假设证明原命题成立,这样的证明方法叫做反证法.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}是集合{x|x=3s+3t , s<t且s,t∈N}中所有的数从小到大排列成的数列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,将数列{an}中各项按照上小下大,左小右大的原则排成如图的等腰直角三角形数表,则a15的值为 . 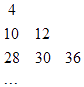
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱柱ABC﹣A1B1C1中,AB=1,BB1=2,求: 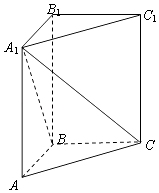
(1)异面直线B1C1与A1C所成角的大小;
(2)四棱锥A1﹣B1BCC1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sinxcosx+2cos2x﹣1,在△ABC中,内角A,B,C的对边分别为a,b,c,且f(B)=1.
sinxcosx+2cos2x﹣1,在△ABC中,内角A,B,C的对边分别为a,b,c,且f(B)=1.
(1)求B;
(2)若 ![]()
![]() =3,求b的取值范围.
=3,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为1的单调递增的等比数列,且满足a3 , ![]() 成等差数列.
成等差数列.
(1)求{an}的通项公式;
(2)若bn=log3(anan+1)(n∈N*),求数列{anbn}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com