
【题目】在几何体![]() 中,如图,四边形
中,如图,四边形![]() 为平行四边形,
为平行四边形,![]() ,平面
,平面![]() 平面
平面![]() 平面
平面![]() ,
,![]()
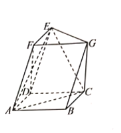
(1)若三棱锥![]() 的体积为1,求
的体积为1,求![]() ;
;
(2)求证:![]()
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过右焦点和短轴一个端点的直线的斜率为
的焦距为2,过右焦点和短轴一个端点的直线的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,记
两点,记![]() 面积的最大值为
面积的最大值为![]() ,证明:
,证明: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以原点为圆心,以短轴长为直径的圆
,且以原点为圆心,以短轴长为直径的圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]()
![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且与圆
,且与圆![]() 没有公共点,设
没有公共点,设![]() 为椭圆
为椭圆![]() 上一点,满足
上一点,满足![]() (
(![]() 为坐标原点),求实数
为坐标原点),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】居民消费价格指数,简称CPI,是一个反映居民家庭一般所购买的消费品和服务项目价格水平变动情况的宏观经济指标.一般来说,CPI的高低直接影响着国家的宏观经济调控措施的出台与力度,下图是国家统计局发布的我国2009年至2018年这十年居民消费价格指数的折线图.
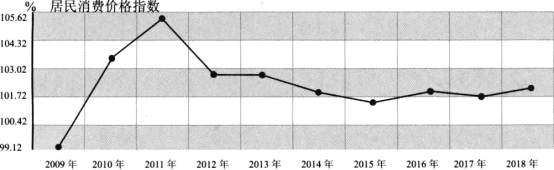
则下列对该折线图分析正确的是( )
A.这十年的居民消费价格指数的中位数为2013年的居民消费价格指数
B.这十年的居民消费价格指数的众数为2015年的居民消费价格指数
C.2009年~2012年这4年居民消费价格指数的方差小于2015年~2018年这4年居民消费价格指数的方差
D.2011年~2013年这3年居民消费价格指数的平均值大于2016年~2018年这3年居民消费价格指数的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】七巧板是中国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪,后清陆以湉《冷庐杂识》卷一中写道“近又有七巧图,其式五,其数七,其变化之式多至千余”在18世纪,七巧板流传到了国外,被誉为“东方魔板”,至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》.完整图案为一正方形(如图):五块等腰直角三角形、一块正方形和一块平行四边形,如果在此正方形中随机取一点,那么此点取自阴影部分的概率是( )
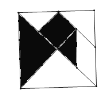
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在单位圆O:x2+y2=1上任取一点P(x,y),圆O与x轴正向的交点是A,设将OA绕原点O旋转到OP所成的角为θ,记x,y关于θ的表达式分别为x=f(θ),y=g(θ),则下列说法正确的是( )
A.x=f(θ)是偶函数,y=g(θ)是奇函数
B.x=f(θ)在![]() 为增函数,y=g(θ)在
为增函数,y=g(θ)在![]() 为减函数
为减函数
C.f(θ)+g(θ)≥1对于![]() 恒成立
恒成立
D.函数t=2f(θ)+g(2θ)的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研团队对![]() 例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中
例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中![]() 名吸烟患者中,重症人数为
名吸烟患者中,重症人数为![]() 人,重症比例约为
人,重症比例约为![]() ;
;![]() 名非吸烟患者中,重症人数为
名非吸烟患者中,重症人数为![]() 人,重症比例为
人,重症比例为![]() .根据以上数据绘制
.根据以上数据绘制![]() 列联表,如下:
列联表,如下:
吸烟人数 | 非吸烟人数 | 总计 | |
重症人数 | 30 | 120 | 150 |
轻症人数 | 100 | 800 | 900 |
总计 | 130 | 920 | 1050 |
(1)根据列联表数据,能否在犯错误的概率不超过![]() 的前提下认为新冠肺炎重症和吸烟有关?
的前提下认为新冠肺炎重症和吸烟有关?
(2)已知每例重症患者平均治疗费用约为![]() 万元,每例轻症患者平均治疗费用约为
万元,每例轻症患者平均治疗费用约为![]() 万元.现有吸烟确诊患者20人,记这
万元.现有吸烟确诊患者20人,记这![]() 名患者的治疗费用总和为
名患者的治疗费用总和为![]() ,求
,求![]() .
.
附:
|
|
|
|
|
|
|
|
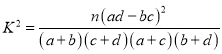
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了有效地加强高中生自主管理能力,推出了一系列措施,其中自习课时间的自主管理作为重点项目,学校有关处室制定了“高中生自习课时间自主管理方案”.现准备对该“方案”进行调查,并根据调查结果决定是否启用该“方案”,调查人员分别在各个年级随机抽取若干学生对该“方案”进行评分,并将评分分成![]() ,
,![]() ,
,![]() ,
,![]() 七组,绘制成如图所示的频率分布直方图.
七组,绘制成如图所示的频率分布直方图.
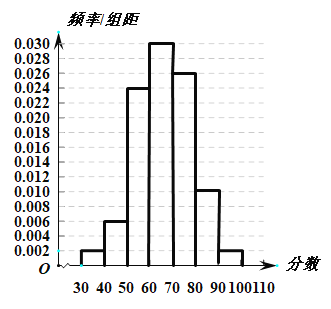
相关规则为①采用百分制评分,![]() 内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于
内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于![]() 即可启用该“方案”;③用样本的频率代替概率.
即可启用该“方案”;③用样本的频率代替概率.
(1)从该校学生中随机抽取1人,求被抽取的这位同学非常满意该“方案”的概率,并根据频率分布直方图求学生对该“方案”评分的中位数.
(2)根据所学统计知识,判断该校是否启用该“方案”,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com