
分析 设两直角边为a,b,斜边长为c,依题意,a+b+$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{2}$+1,利用基本不等式可求得$\sqrt{ab}$≤$\frac{\sqrt{2}}{2}$,从而可求得该直角三角形面积的最大值.
解答 解:设两直角边为a,b,斜边长为c,
则c2=a2+b2,且a+b+$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{2}$+1,
∴$\sqrt{2}$+1=a+b+$\sqrt{{a}^{2}+{b}^{2}}$≥2$\sqrt{ab}$+$\sqrt{2}$$\sqrt{ab}$=(2+$\sqrt{2}$)$\sqrt{ab}$,
即$\sqrt{ab}$≤$\frac{\sqrt{2}}{2}$,当且仅当a=b时取等号.
∴三角形的面积S=$\frac{1}{2}$ab≤$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{4}$,
即Smax=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查基本不等式,依题意,得到a+b+$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{2}$+1是应用基本不等式基础,考查创新与运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∨q | C. | p∧¬q | D. | p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
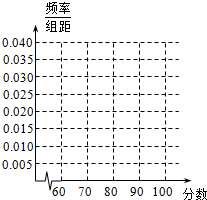 为纪念中国抗日战争胜利70周年,某中学高三年级举办了“铭记历史,开创未来”的抗战历史知识竞赛活动,共有1000名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据频率分布表,解答下列问题:
为纪念中国抗日战争胜利70周年,某中学高三年级举办了“铭记历史,开创未来”的抗战历史知识竞赛活动,共有1000名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据频率分布表,解答下列问题:| 序号 | 分组 | 频数 | 频率 |
| 1 | [60,70) | ① | 0.15 |
| 2 | [70,80) | 20 | 0.2 |
| 3 | [80,90) | 35 | 0.35 |
| 4 | [90,100) | 30 | ② |
| 合计 | 100 | 1 | |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com