
【题目】已知函数f(x)=ex(x2+ax-a),其中a是常数.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若存在实数k,使得关于x的方程f(x)=k在[0,+∞)上有两个不相等的实数根,求k的取值范围.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】
(1)求出![]() ,求出
,求出![]() 的值可得切点坐标,求出
的值可得切点坐标,求出![]() 的值,可得切线斜率,利用点斜式可得曲线
的值,可得切线斜率,利用点斜式可得曲线![]() 在点
在点![]() 处的切线方程;(Ⅱ)利用导数研究函数的单调性,可得函数
处的切线方程;(Ⅱ)利用导数研究函数的单调性,可得函数![]() 是
是![]() 上的减函数,是
上的减函数,是![]() 上的增函数,函数
上的增函数,函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ., 且当
., 且当![]() 时,有
时,有![]()
![]() .,从而可求
.,从而可求![]() 的取值范围.
的取值范围.
(Ⅰ)由![]() 可得
可得
![]() .
.
当![]() 时,
时,![]() ,
,![]() .
.
所以 曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() .
.
(Ⅱ) ![]() ,
,
解得![]() 或
或![]() .
.
当![]() ,即
,即![]() 时,在区间
时,在区间![]() 上,
上,![]() ,
,
所以![]() 是
是![]() 上的增函数.
上的增函数.
所以 方程![]() 在
在![]() 上不可能有两个不相等的实数根.
上不可能有两个不相等的实数根.
当![]() ,即
,即![]() 时,
时,![]() 随
随![]() 的变化情况如下表
的变化情况如下表
|
|
|
|
|
|
|
|
|
|
|
| ↘ |
| ↗ |
由上表可知函数![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
因为 函数![]() 是
是![]() 上的减函数,是
上的减函数,是![]() 上的增函数,
上的增函数,
且当![]() 时,有
时,有![]()
![]() .
.
所以 要使方程![]() 在
在![]() 上有两个不相等的实数根,
上有两个不相等的实数根,![]() 的取值范围必须是
的取值范围必须是
![]() .
.


科目:高中数学 来源: 题型:
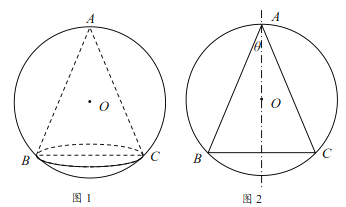
【题目】某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆![]() 及其内接等腰三角形
及其内接等腰三角形![]() 绕底边
绕底边![]() 上的高所在直线
上的高所在直线![]() 旋转180°而成,如图2.已知圆
旋转180°而成,如图2.已知圆![]() 的半径为
的半径为![]() ,设
,设![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)为了达到最佳观赏效果,要求圆锥的侧面积![]() 最大.求
最大.求![]() 取得最大值时腰
取得最大值时腰![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,长半轴长为短轴长的b倍,A,B分别为椭圆C的上、下顶点,点
,长半轴长为短轴长的b倍,A,B分别为椭圆C的上、下顶点,点![]() .
.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 若直线MA,MB与椭圆C的另一交点分别为P,Q,证明:直线PQ过定点.
若直线MA,MB与椭圆C的另一交点分别为P,Q,证明:直线PQ过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空格内填入“充分非必要”或“必要非充分”或“充要”或“既非充分又非必要”.
(1)“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(2)“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(3)已知![]() ,
,![]() ,“
,“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(4)“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(5)“![]() ”是“AB”的________条件;
”是“AB”的________条件;
(6)“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(7)“集合AB”是“![]() ”的________条件;
”的________条件;
(8)已知![]() ,“
,“![]() ”是“
”是“![]() ”的________条件.
”的________条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司欲将一批海产品从A地运往B地,现有汽车、火车、飞机三种运输工具可供选择,这三种工具的主要参考数据如下:
运输工具 | 途中速度( | 途中费用(元/ | 装卸时间( | 装卸费用(元/ |
汽车 | 50 | 80 | 2 | 200 |
火车 | 100 | 40 | 3 | 400 |
飞机 | 200 | 200 | 3 | 800 |
若这批海产品在运输过程中的损耗为300元/![]() ,问采用哪种运输方式比较好,即运输过程中的费用与损耗之和最小.
,问采用哪种运输方式比较好,即运输过程中的费用与损耗之和最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,两焦点与短轴的一个顶点构成等腰直角三角形,且点
,两焦点与短轴的一个顶点构成等腰直角三角形,且点 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如图所示,过椭圆的左焦点作直线![]() (斜率存在且不为0)交椭圆
(斜率存在且不为0)交椭圆![]() 于
于![]() 两点,过右焦点作直线
两点,过右焦点作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,且
两点,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,动点
,动点![]() (异于
(异于![]() )在椭圆上运动.
)在椭圆上运动.
①证明: ![]() 为常数;
为常数;
②当![]() 时,利用上述结论求
时,利用上述结论求![]() 面积的取值范围.
面积的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款击鼓小游戏的规则如下:每轮游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每轮游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为![]() ,且各次击鼓是否出现音乐相互独立.
,且各次击鼓是否出现音乐相互独立.
(1)玩三轮游戏,至少有一轮出现音乐的概率是多少?
(2)设每轮游戏获得的分数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
试销单价 | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量 |
| 84 | 83 | 80 | 75 | 68 |
已知![]() .
.
(1)求出![]() 的值;
的值;
(2)已知变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;可供选择的数据:
;可供选择的数据:![]() ,
,![]() ;
;
(3)用![]() 表示用(2)中所求的线性回归方程得到的与
表示用(2)中所求的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数
称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(参考公式:线性回归方程中![]() 的最小二乘估计分别为
的最小二乘估计分别为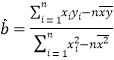 ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com