
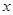 %,则销售量将减少
%,则销售量将减少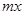 %,且该化工产品每吨的价格上涨幅度不超过
%,且该化工产品每吨的价格上涨幅度不超过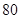 %,
%,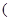 其中
其中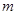 为正常数
为正常数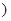

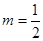 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?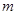 的取值范围.
的取值范围.科目:高中数学 来源:不详 题型:解答题
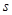 平方米,矩形一边的长为
平方米,矩形一边的长为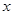 米(如图所示)
米(如图所示)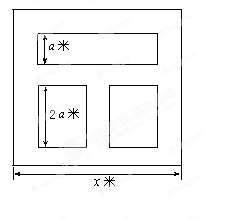
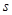 表示为
表示为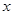 的函数;
的函数;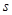 取得最大值.
取得最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
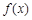 与
与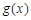 ,如果对任意
,如果对任意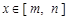 ,均有
,均有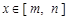 ,则称
,则称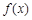 与
与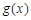 在 [ m,n ] 上是友好的,否则称
在 [ m,n ] 上是友好的,否则称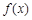 与
与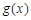 在 [ m,n ]是不友好的.现有两个函数
在 [ m,n ]是不友好的.现有两个函数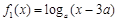 与
与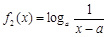 (a > 0且
(a > 0且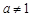 ),给定区间
),给定区间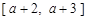 .
.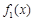 与
与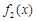 在给定区间
在给定区间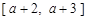 上都有意义,求a的取值范围;
上都有意义,求a的取值范围;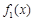 与
与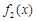 在给定区间
在给定区间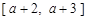 上是否友好.
上是否友好.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
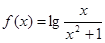 ,有下列结论:①函数
,有下列结论:①函数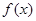 的定义域是(0,+∞);②函数
的定义域是(0,+∞);②函数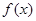 是奇函数;③函数
是奇函数;③函数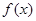 的最小值为-
的最小值为-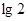 ;④当
;④当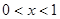 时,函数
时,函数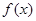 是增函数;当
是增函数;当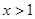 时,函数
时,函数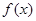 是减函数.
是减函数.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
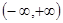 上的偶函数
上的偶函数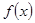 满足
满足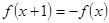 ,且在
,且在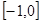 上是增函数,下面关于
上是增函数,下面关于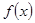 的判断:
的判断: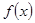 关于点P(
关于点P(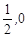 )对称 ②
)对称 ②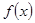 的图像关于直线
的图像关于直线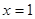 对称;
对称;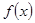 在[0,1]上是增函数; ④
在[0,1]上是增函数; ④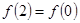 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com