
【题目】已知数列![]() 中,
中,![]() ,前n项和为
,前n项和为![]() ,且
,且![]() .
.
(1)求![]() ;
;
(2)证明数列![]() 为等差数列,并写出其通项公式;
为等差数列,并写出其通项公式;
(3)设![]() ,试问是否存在正整数p,q(其中
,试问是否存在正整数p,q(其中![]() ),使
),使![]()
![]()
![]() 成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
【答案】(1)![]() (2)证明见解析;
(2)证明见解析;![]() (3)存在唯一正整数数对
(3)存在唯一正整数数对![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() 成等比数列;详见解析
成等比数列;详见解析
【解析】
(1)令![]() ,即可求
,即可求![]() ;
;
(2)根据等差数列的等差中项法即可证明数列![]() 为等差数列,并写出其通项公式;
为等差数列,并写出其通项公式;
(3)根据等比数列的定义和通项公式,分类讨论![]() ,通过数列的单调性求出数列最值,结合题意判断求解,即可得到结论.
,通过数列的单调性求出数列最值,结合题意判断求解,即可得到结论.
(1)令![]() ,则
,则![]() .
.
(2)由![]() ,即
,即![]() ,①
,①
得![]() .②
.②
②-①,得![]() .③
.③
于是,![]() .④
.④
③+④,得![]() ,即
,即![]() .
.
又![]() ,
,![]() ,
,![]() ,
,
所以,数列![]() 是以0为首项,1为公差的等差数列.
是以0为首项,1为公差的等差数列.
所以,![]() .
.
(3)假设存在正整数数组![]() (其中
(其中![]() ),使
),使![]()
![]()
![]() 成等比数列,
成等比数列,
则![]()
![]()
![]() 成等差数列,于是
成等差数列,于是![]() .
.
![]() 时,
时,![]() ,故数列
,故数列![]() 为递减数列,
为递减数列,
![]() 时,
时,![]() ,故数列
,故数列![]() 为递减数列,
为递减数列,
![]() ,
,![]() ,即
,即![]()
![]() 时,
时,![]() .
.
又当![]() 时,
时,![]() ,故无正整数q使得
,故无正整数q使得![]() 成立.
成立.
综上得,存在唯一正整数数对![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“3号”车的概率分别为P1,P2,则( )
A. P1P2=![]() B. P1=P2=
B. P1=P2=![]() C. P1+P2=
C. P1+P2=![]() D. P1<P2
D. P1<P2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县共有户籍人口60万,经统计,该县60岁及以上、百岁以下的人口占比![]() ,百岁及以上老人15人.现从该县60岁及以上、百岁以下的老人中随机抽取230人,得到如下频数分布表:
,百岁及以上老人15人.现从该县60岁及以上、百岁以下的老人中随机抽取230人,得到如下频数分布表:
年龄段(岁) |
|
|
|
|
人数(人) | 125 | 75 | 25 | 5 |
(1)从样本中70岁及以上老人中,采用分层抽样的方法抽取21人,进一步了解他们的生活状况,则80岁及以上老人应抽多少人?
(2)从(1)中所抽取的80岁及以上老人中,再随机抽取2人,求抽到90岁及以上老人的概率;
(3)该县按省委办公厅、省人民政府办公厅《关于加强新时期老年人优待服务工作的意见》精神,制定如下老年人生活补贴措施,由省、市、县三级财政分级拨款:
①本县户籍60岁及以上居民,按城乡居民养老保险实施办法每月领取55元基本养老金;
②本县户籍80岁及以上老年人额外享受高龄老人生活补贴;
(a)百岁及以上老年人,每人每月发放345元的生活补贴;
(b)90岁及以上、百岁以下老年人,每人每月发放200元的生活补贴;
(c)80岁及以上、90岁以下老年人,每人每月发放100元的生活补贴.
试估计政府执行此项补贴措施的年度预算.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,点E在AB上,AE=2EB=2,且DE⊥AB.以DE为折痕把△ADE折起,使点A到达点F的位置,且∠FEB=60°.
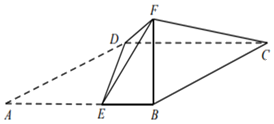
(1)求证:平面BFC⊥平面BCDE;
(2)若直线DF与平面BCDE所成角的正切值为![]() ,求二面角E﹣DF﹣C的正弦值.
,求二面角E﹣DF﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列a,b,c是各项均为正数的等差数列,公差为d(d>0).在a,b之间和b,c之间共插入n个实数,使得这n+3个数构成等比数列,其公比为q.
(1)求证:|q|>1;
(2)若a=1,n=1,求d的值;
(3)若插入的n个数中,有s个位于a,b之间,t个位于b,c之间,且s,t都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用a,c,n表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的正视图是一个底边长为4腰长为3的等腰三角形,图1、图2分别是四棱锥
的正视图是一个底边长为4腰长为3的等腰三角形,图1、图2分别是四棱锥![]() 的侧视图和俯视图.
的侧视图和俯视图.
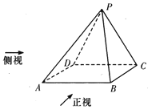
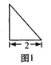
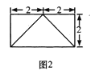
(1)求证:![]() ;
;
(2)求四棱锥![]() 的体积及侧面积.
的体积及侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】边长为![]() 的等边三角形内任一点到三边距离之和为定值,则这个定值为
的等边三角形内任一点到三边距离之和为定值,则这个定值为![]() ;推广到空间,棱长为
;推广到空间,棱长为![]() 的正四面体内任一点到各面距离之和为___________________.
的正四面体内任一点到各面距离之和为___________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com