
| 本科 | 研究生 | 合计 | |
| 35岁以下 | 5 | 2 | 7 |
| 35~50岁(含35岁和50岁) | 17 | 3 | 20 |
| 50岁以上 | 2 | 1 | 3 |
| 6 |
| 30 |
| 1 |
| 5 |
| 1 |
| 5 |
| 12 |
| 15 |
| 4 |
| 5 |
| 4 |
| 5 |


科目:高中数学 来源: 题型:
| 1 |
| 100 |
| 99 |
| 100 |
| 294 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
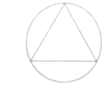 某人随机地向如图所示的正三角形及其外接圆区域内部设计(不包括三角形及其外接圆的边界),则针孔到正三角形内部(不包括边界)的概率为( )
某人随机地向如图所示的正三角形及其外接圆区域内部设计(不包括三角形及其外接圆的边界),则针孔到正三角形内部(不包括边界)的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
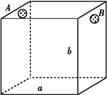 为处理含有某种杂质的污水,要制造一个底宽为2米的无盖长方体沉淀箱(如图),污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a、b的乘积ab成反比,现有制箱材料60平方米,当a、b各为( )米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?
为处理含有某种杂质的污水,要制造一个底宽为2米的无盖长方体沉淀箱(如图),污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a、b的乘积ab成反比,现有制箱材料60平方米,当a、b各为( )米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?| A、a=2,b=9 |
| B、a=9,b=2 |
| C、a=3,b=6 |
| D、a=6,b=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:

| A、计算50个学生的平均成绩 |
| B、计算50个学生中不及格的人数 |
| C、计算50个学生中及格的人数 |
| D、计算50个学生的总成绩 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com