定义在R上的函数y=f(x)是增函数,且函数y=f(x-2)的图象关于(2,0)成中心对称,设s,t满足不等式f(s2-4s)≥-f(4t-t2),若-2≤s≤2时,则3t+s的范围是 .
【答案】
分析:先确定y=f(x)函数图象关于(0,0)点对称,再利用函数是增函数,将不等式f(s
2-4s)≥-f(4t-t
2),化为具体不等式,利用可行域,即可求得3t+s的范围
解答: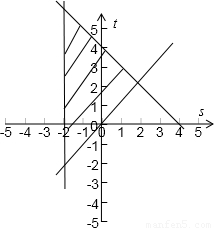
解:y=f(x-2)的图象相当于y=f(x)函数图象向右移了2个单位.
又由于y=f(x-2)图象关于(2,0)点对称,向左移2个单位,即表示y=f(x)函数图象关于(0,0)点对称.
所以-f(4t-t
2)=f(t
2-4t)
即不等式f(s
2-4s)≥-f(4t-t
2),等价于f(s
2-4s)≥f(t
2-4t)
因为函数y=f(x)是增函数,所以s
2-4s≥t
2-4t
移项得:s
2-4s-t
2+4t≥0,即:(s-t)(s+t-4)≥0
得:s≥t且s+t≥4或s≤t且s+t≤4
可行域如图所示,则当s=-2,t=-2时,3t+s有最小值是-6-2=-8
当s=-2,t=6时,3t+s有最大值是18-2=16
故3t+s范围是[-8,16]
故答案为:[-8,16]
点评:本题考查函数的性质,考查不等式的化简,考查线性规划知识,考查学生分析解决问题的能力,属于中档题.

 解:y=f(x-2)的图象相当于y=f(x)函数图象向右移了2个单位.
解:y=f(x-2)的图象相当于y=f(x)函数图象向右移了2个单位.
