
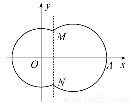
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上.圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).
(1)求圆弧C2的方程.
(2)曲线C上是否存在点P,满足PA=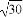 PO?若存在,指出有几个这样的点;若不存在,请说明理由.
PO?若存在,指出有几个这样的点;若不存在,请说明理由.
(1) (x-14)2+y2=225(5≤x≤29) (2) 不存在,理由见解析
【解析】(1)圆弧C1所在圆的方程为x2+y2=169,令x=5,解得M(5,12),N(5, -12).
则线段AM中垂线的方程为y-6=2(x-17),令y=0,得圆弧C2所在圆的圆心为(14,0),
又圆弧C2所在圆的半径为r2=29-14=15,所以圆弧C2的方程为(x-14)2+y2=225(5≤x≤29).
(2)假设存在这样的点P(x,y),
则由PA=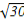 PO,得x2+y2+2x-29=0,
PO,得x2+y2+2x-29=0,
由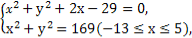
解得x=-70(舍去).
由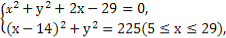
解得x=0(舍去),
综上知,这样的点P不存在.
【误区警示】求圆弧C2的方程时经常遗漏x的取值范围,其错误原因是将圆弧习惯认为或误认为圆.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十第八章第一节练习卷(解析版) 题型:解答题
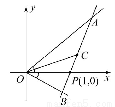
如图,射线OA,OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA,OB于A,B两点,当AB的中点C恰好落在直线y= x上时,求直线AB的方程.
x上时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十六第八章第七节练习卷(解析版) 题型:选择题
若抛物线y2=2px(p>0)的焦点在圆x2+y2+2x-3=0上,则p=( )
(A) (B)1 (C)2 (D)3
(B)1 (C)2 (D)3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十五第八章第六节练习卷(解析版) 题型:填空题
过双曲线的右焦点F作实轴所在直线的垂线,交双曲线于A,B两点,设双曲线的左顶点为M,若点M在以AB为直径的圆的内部,则此双曲线的离心率e的取值范围为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十五第八章第六节练习卷(解析版) 题型:选择题
设双曲线的一个焦点为F,虚轴的一个端点为B,如果直线FB与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
(A)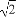 (B)
(B)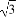 (C)
(C)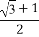 (D)
(D)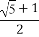
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:选择题
过点A(11,2)作圆x2+y2+2x-4y-164=0的弦,其中弦长为整数的共有( )
(A)16条 (B)17条 (C)32条 (D)34条
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:选择题
圆心在y轴上,半径为1,且过点(1,2)的圆的方程为( )
(A)x2+(y-2)2=1 (B)x2+(y+2)2=1
(C)(x-1)2+(y-3)2=1 (D)x2+(y-3)2=1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十三第八章第四节练习卷(解析版) 题型:解答题
过点Q(-2,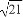 )作圆O:x2+y2=r2(r>0)的切线,切点为D,且|QD|=4.
)作圆O:x2+y2=r2(r>0)的切线,切点为D,且|QD|=4.
(1)求r的值.
(2)设P是圆O上位于第一象限内的任意一点,过点P作圆O的切线l,且l交x轴于点A,交y轴于点B,设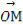 =
=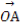 +
+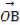 ,求|
,求|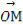 |的最小值(O为坐标原点).
|的最小值(O为坐标原点).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十一第八章第二节练习卷(解析版) 题型:选择题
对任意实数a,直线y=ax-3a+2所经过的定点是( )
(A)(2,3) (B)(3,2)
(C)(-2,3) (D)(3,-2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com