
【题目】如图,四棱锥![]() 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的![]() 倍,
倍,![]() 为侧棱
为侧棱![]() 上的点.
上的点.
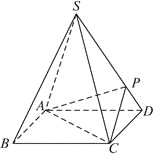
(1)求证:![]() .
.
(2)若![]() ⊥平面
⊥平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.
【答案】(1)详见解析(2)30°(3)SE∶EC=2∶1
【解析】试题分析:(1)连BD,设AC交于BD于O,由题意知SO⊥平面ABCD.以O为坐标原点,![]() 分别为x轴、y轴、z轴正方向,建立坐标系O-xyz,设底面边长为a,求出高SO,从而得到点S与点C和D的坐标,求出向量
分别为x轴、y轴、z轴正方向,建立坐标系O-xyz,设底面边长为a,求出高SO,从而得到点S与点C和D的坐标,求出向量![]() 与
与![]() ,计算它们的数量积,从而证明出OC⊥SD,则AC⊥SD;(2)根据题意先求出平面PAC的一个法向量
,计算它们的数量积,从而证明出OC⊥SD,则AC⊥SD;(2)根据题意先求出平面PAC的一个法向量![]() 和平面DAC的一个法向量
和平面DAC的一个法向量![]() ,设所求二面角为θ,则
,设所求二面角为θ,则![]() ,从而求出二面角的大小;(3)在棱SC上存在一点E使BE∥平面PAC,根据(Ⅱ)知
,从而求出二面角的大小;(3)在棱SC上存在一点E使BE∥平面PAC,根据(Ⅱ)知![]() 是平面PAC的一个法向量,设
是平面PAC的一个法向量,设![]() ,求出
,求出![]() ,根据
,根据![]() 可求出t的值,从而即当SE:EC=2:1时,
可求出t的值,从而即当SE:EC=2:1时,![]() ,而BE不在平面PAC内,故BE∥平面PAC
,而BE不在平面PAC内,故BE∥平面PAC
试题解析:(1)证明:连BD,设AC交BD于O,由题意SO⊥AC.在正方形ABCD中,AC⊥BD,所以AC⊥平面SBD,得AC⊥SD
(2)设正方形边长a,则![]() .
.
又![]() ,所以∠SDO=60°.
,所以∠SDO=60°.
连OP,由(1)知AC⊥平面SBD,所以AC⊥OP,且AC⊥OD.所以∠POD是二面角P-AC-D的平面角.
由SD⊥平面PAC,知SD⊥OP,所以∠POD=30°,
即二面角P-AC-D的大小为30°
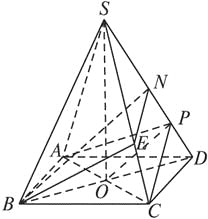
(3)在棱SC上存在一点E,使BE∥平面PAC.
由(2)可得![]() ,故可在SP上取一点N,使PN=PD.过N作PC的平行线与SC的交点即为E.连BN,在△BDN中知BN∥PO.
,故可在SP上取一点N,使PN=PD.过N作PC的平行线与SC的交点即为E.连BN,在△BDN中知BN∥PO.
又由于NE∥PC,故平面BEN∥平面PAC,得BE∥平面PAC.
由于SN∶NP=2∶1,故SE∶EC=2∶1


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ) ![]() 部分图象如图所示.
部分图象如图所示.
(Ⅰ)求f(x)的最小正周期及解析式;
(Ⅱ)设g(x)=f(x)﹣cos2x,求函数g(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.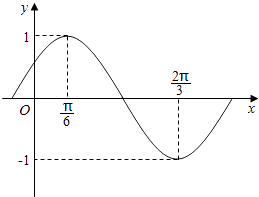
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙O:x2+y2=1和点M(4,2).
(Ⅰ)过点M向⊙O引切线l,求直线l的方程;
(Ⅱ)求以点M为圆心,且被直线y=2x﹣1截得的弦长为4的⊙M的方程;
(Ⅲ)设P为(Ⅱ)中⊙M上任一点,过点P向⊙O引切线,切点为Q.试探究:平面内是否存在一定点R,使得 ![]() 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.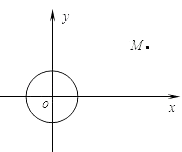
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx)+b(A>0,ω>0)的最大值为2,最小值为0,其图象相邻两对称轴间的距离为2,则f(1)+f(2)+…+f(2008)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),|
=(cosβ,sinβ),| ![]() ﹣
﹣ ![]() |=
|= ![]() .
.
(1)求cos(α﹣β)的值;
(2)若0<α< ![]() ,﹣
,﹣ ![]() <β<0,且sinβ=﹣
<β<0,且sinβ=﹣ ![]() ,求sinα的值.
,求sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
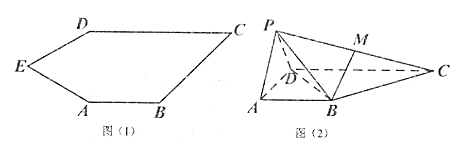
【题目】如图(1)五边形![]() 中,
中, ![]()
![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() ,如图(2),点
,如图(2),点![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若四棱柱![]() 的体积为
的体积为![]() ,求四面体
,求四面体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com