在等比数列{an}(n∈N*)中,a1>1,公比q>0.设bn=log2an,且b1+b3+b5=6,b1b3b5=0.
(1)求证:数列{bn}是等差数列;
(2)求{bn}的前n项和Sn及{an}的通项an;
(3)试比较an与Sn的大小.
(1)证明:∵b
n=log
2a
n,
∴b
n+1-b
n=log
2
=log
2q为常数.
∴数列{b
n}为等差数列且公差d=log
2q.
(2)解:∵b
1+b
3+b
5=6,∴b
3=2.
∵a
1>1,∴b
1=log
2a
1>0.
∵b
1b
3b
5=0,∴b
5=0.
∴
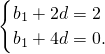
解得

∴S
n=4n+

×(-1)=
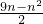
.
∵
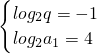
∴
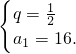
∴a
n=2
5-n(n∈N
*).
(3)解:显然a
n=2
5-n>0,当n≥9时,S
n=

≤0.
∴n≥9时,a
n>S
n.
∵a
1=16,a
2=8,a
3=4,a
4=2,a
5=1,a
6=

,a
7=

,a
8=

,S
1=4,S
2=7,S
3=9,S
4=10,S
5=10,S
6=9,S
7=7,S
8=4,
∴当n=3,4,5,6,7,8时,a
n<S
n;
当n=1,2或n≥9时,a
n>S
n.
分析:(1)由题设知b
n+1-b
n=log
2
=log
2q为常数.所以数列{b
n}为等差数列且公差d=log
2q.
(2)根据题设条件先求首项和公差及公比.然后再求{b
n}的前n项和S
n及{a
n}的通项a
n.
(3)根据题设条件分情况讨论,能够比较a
n与S
n的大小.
点评:本题主要考查了数列的基本知识和分类讨论的思想.

 =log2q为常数.
=log2q为常数.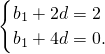 解得
解得
 ×(-1)=
×(-1)=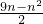 .
.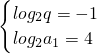 ∴
∴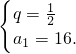
 ≤0.
≤0. ,a7=
,a7= ,a8=
,a8= ,S1=4,S2=7,S3=9,S4=10,S5=10,S6=9,S7=7,S8=4,
,S1=4,S2=7,S3=9,S4=10,S5=10,S6=9,S7=7,S8=4, =log2q为常数.所以数列{bn}为等差数列且公差d=log2q.
=log2q为常数.所以数列{bn}为等差数列且公差d=log2q.

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案