
【题目】已知①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 在如右图所示的程序框图中,如果输入
在如右图所示的程序框图中,如果输入![]() ,而输出
,而输出![]() ,则在空白处可填入( )
,则在空白处可填入( )
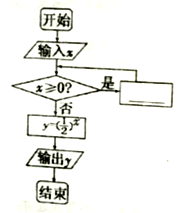
A.①②③ B.②③ C.③④ D.②③④
【答案】D
【解析】
试题:①若填入![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
…
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,不满足进行循环的条件,
时,不满足进行循环的条件,
此时输出![]() ,不满足题目要求;
,不满足题目要求;
②若填入![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,不满足进行循环的条件,
时,不满足进行循环的条件,
此时输出![]() ,满足题目要求;
,满足题目要求;
③若填入![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,满足进行循环的条件
时,满足进行循环的条件![]() ,,
,,
当![]() 时,不满足进行循环的条件,
时,不满足进行循环的条件,
此时输出![]() ,满足题目要求;
,满足题目要求;
④若填入![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,满足进行循环的条件,
时,满足进行循环的条件,![]() ,
,
当![]() 时,不满足进行循环的条件,
时,不满足进行循环的条件,
此时输出![]() ,满足题目要求;
,满足题目要求;
综上所述,图中“?”处可填入的算法语句是②③④,
故答案为:②③④


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:高中数学 来源: 题型:
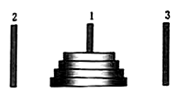
【题目】如图所示,有三根针和套在一根针上的![]() 个金属片,按下列规则,把金属片从一根针上全部移到另一根针上.
个金属片,按下列规则,把金属片从一根针上全部移到另一根针上.
(1)每次只能移动一个金属片;
(2)在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.
将![]() 个金属片从1号针移到3号针最少需要移动的次数记为
个金属片从1号针移到3号针最少需要移动的次数记为![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为确定下一年度投入某种产品的生产所需的资金,需了解每投入2千万资金后,工人人数![]() (单位:百人)对年产能
(单位:百人)对年产能![]() (单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
(单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
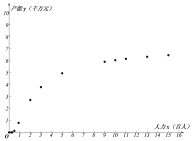
(1)根据散点图判断:![]() 与
与![]() 哪一个适宜作为年产能
哪一个适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型?并说明理由?
的回归方程类型?并说明理由?
(2)根据(1)的判断结果及相关的计算数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)现该企业共有2000名生产工人,资金非常充足,为了使得年产能达到最大值,则下一年度共需投入多少资金(单位:千万元)?
附注:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为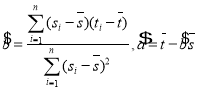 ,(说明:
,(说明:![]() 的导函数为
的导函数为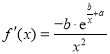 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
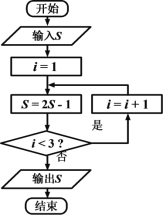
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等腰直角三角形![]() 的斜边AB为正四面体
的斜边AB为正四面体![]() 侧棱,直角边AE绕斜边AB旋转,则在旋转的过程中,有下列说法:
侧棱,直角边AE绕斜边AB旋转,则在旋转的过程中,有下列说法:

(1)四面体E![]() BCD的体积有最大值和最小值;
BCD的体积有最大值和最小值;
(2)存在某个位置,使得![]() ;
;
(3)设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() ;
;
(4)AE的中点M与AB的中点N连线交平面BCD于点P,则点P的轨迹为椭圆.
其中,正确说法的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() ,以原点为极点,
,以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为曲线
的极坐标方程为曲线![]() .
.
(Ⅰ)写出直线![]() 的参数方程及曲线
的参数方程及曲线![]() 的普通方程;
的普通方程;
(Ⅱ)求直线![]() 和曲线
和曲线![]() 的两个交点到点
的两个交点到点![]() 的距离的和与积.
的距离的和与积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2016年1月至2018年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
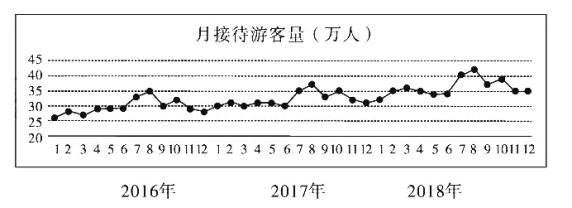
根据该折线图,判断下列结论:
(1)月接待游客量逐月增加;
(2)年接待游客量逐年增加;
(3)各年的月接待游客量高峰期大致在7,8月;
(4)各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳.
其中正确结论的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 、
、![]() 是两个相交平面,则在下列命题中,真命题的序号为( )
是两个相交平面,则在下列命题中,真命题的序号为( )
①若直线![]() ,则在平面
,则在平面![]() 内一定不存在与直线
内一定不存在与直线![]() 平行的直线.
平行的直线.
②若直线![]() ,则在平面
,则在平面![]() 内一定存在无数条直线与直线
内一定存在无数条直线与直线![]() 垂直.
垂直.
③若直线![]() ,则在平面
,则在平面![]() 内不一定存在与直线
内不一定存在与直线![]() 垂直的直线.
垂直的直线.
④若直线![]() ,则在平面
,则在平面![]() 内一定存在与直线
内一定存在与直线![]() 垂直的直线.
垂直的直线.
A. ①③ B. ②③ C. ②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为2,离心率为
的短轴长为2,离心率为![]() ,
,![]() ,
,![]() 分别是椭圆的右顶点和下顶点.
分别是椭圆的右顶点和下顶点.
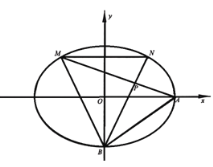
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() 是椭圆
是椭圆![]() 内一点,直线
内一点,直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,直线
,直线![]() 分别交椭圆于
分别交椭圆于![]() 两点,记
两点,记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() .
.
①若![]() 两点关于
两点关于![]() 轴对称,求直线
轴对称,求直线![]() 的斜率;
的斜率;
②证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com