
【题目】已知函数 ![]() (a>0,a≠1).
(a>0,a≠1).
(1)判断函数f(x)的奇偶性;
(2)判断函数f(x)在(1,+∞)上的单调性,并给出证明;
(3)当x∈(n,a﹣2)时,函数f(x)的值域是(1,+∞),求实数a与n的值.
【答案】
(1)解:由 ![]() 得函数f(x)的定义域为(1,+∞)∪(﹣∞,﹣1),
得函数f(x)的定义域为(1,+∞)∪(﹣∞,﹣1),
又 ![]()
所以f(x)为奇函数
(2)解:由(1)及题设知: ![]() ,设
,设 ![]() ,
,
∴当x1>x2>1时, ![]() ∴t1<t2.
∴t1<t2.
当a>1时,logat1<logat2,即f(x1)<f(x2).
∴当a>1时,f(x)在(1,+∞)上是减函数.
同理当0<a<1时,f(x)在(1,+∞)上是增函数
(3)解:①当n<a﹣2≤﹣1时,有0<a<1.
由(2)可知:f(x)在(n,a﹣2)为增函数,
由其值域为(1,+∞)知 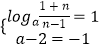 ,无解
,无解
②当1≤n<a﹣2时,有a>3.由(2)知:f(x)在(n,a﹣2)为减函数,
由其值域为(1,+∞)知 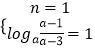
得 ![]() ,n=1
,n=1
【解析】(1)先求函数的定义域看是否关于原点对称,然后在用奇偶函数的定义判断,要注意到代入﹣x时,真数是原来的倒数,这样就不难并判断奇偶性.(2)用单调性的定义进行证明,首先在所给的区间上任取两个自变量看真数的大小关系,然后在根据底的不同判断函数单调性.(3)要根据第二问的结论,进行分类讨论,解出两种情况下的实数a与n的值.


科目:高中数学 来源: 题型:
【题目】在某校歌咏比赛中,甲班、乙班、丙班、丁班均可从![]() 、
、![]() 、
、![]() 、
、![]() 四首不同曲目中任选一首.
四首不同曲目中任选一首.
(1)求甲、乙两班选择不同曲目的概率;
(2)设这四个班级总共选取了![]() 首曲目,求
首曲目,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算题
(1)已知集合A={x|3<x<7},B={x|2<x<10},求A∪B,A∩B,RA
(2)计算下列各式 ① ![]()
②(2a ![]() b
b ![]() )(﹣6a
)(﹣6a ![]() b
b ![]() )÷(﹣3a
)÷(﹣3a ![]() b
b ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数g(x)=3x , h(x)=9x .
(1)解方程:h(x)﹣8g(x)﹣h(1)=0;
(2)令p(x)= ![]() ,求值:p(
,求值:p( ![]() )+p(
)+p( ![]() )+…+p(
)+…+p( ![]() )+p(
)+p( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题。
(1)已知函数f(x)=4x2﹣kx﹣8在[5,20]上具有单调性,求实数k的取值范围.
(2)关于x的方程mx2+2(m+3)x+2m+14=0有两个不同的实根,且一个大于4,另一个小于4,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 图像向右平移
图像向右平移![]() 个单位得到
个单位得到![]() 的图像,将函数
的图像,将函数![]() 图像向左平移
图像向左平移![]() 个单位得到
个单位得到![]() 的图像,若令
的图像,若令![]() ,则
,则
(Ⅰ)函数![]() 的最小正周期、单调递增区间;
的最小正周期、单调递增区间;
(Ⅱ)求![]() 在区间
在区间![]() 上的值域.
上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com