
【题目】某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据). 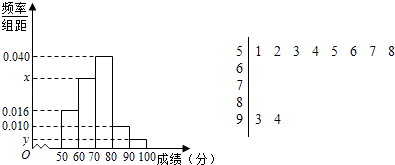
(1)求样本容量n和频率分布直方图中的x,y的值;
(2)估计本次竞赛学生成绩的中位数和平均分;
(3)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中至少有一人得分在[90,100]内的频率.
【答案】
(1)解:由题意可知,样本容量n= ![]() =50,y=
=50,y= ![]() =0.004,x=0.100﹣0.004﹣0.010﹣0.016﹣0.040=0.030
=0.004,x=0.100﹣0.004﹣0.010﹣0.016﹣0.040=0.030
(2)解:设本次竞赛学生成绩的中位数为m,平均分为 ![]() ,
,
则[0.016+0.03+(m﹣70)×0.040]×10=0.5,解得m=71,
![]() =(55×0.016+65×0.030+75×0.040+85×0.010+95×0.004]×10=70.6
=(55×0.016+65×0.030+75×0.040+85×0.010+95×0.004]×10=70.6
(3)解:由题意可知,分数在[80,90)内的学生有5人,记这5人分别为a1,a2,a3,a4,a5,
分数在[90,100]内的学生有2人,记这2人分别为b1,b2.抽取的2名学生的所有情况有21种,
分别为:(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a1,b1),(a1,b2),(a2,a3),
(a2,a4),(a2,a5),(a2,b1),(a2,b2),(a3,a4),(a3,a5),(a3,b1),
(a3,b2),(a4,a5),(a4,b1),(a4,b2),(a5,b1),(a5,b2),(b1,b2).
其中2名同学的分数都不在[90,100]内的情况有10种,分别为:
(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a2,a3),(a2,a4),(a2,a5),
(a3,a4),(a3,a5),(a4,a5).
∴所抽取的2名学生中至少有一人得分在[90,100]内的概率P=1﹣ ![]() =
= ![]()
【解析】(1)由样本容量和频数频率的关系易得答案;(2)根据平均数的定义和中位数的定义即可求出.(3)由题意可知,分数在[80,90)内的学生有5人,记这5人分别为a1 , a2 , a3 , a4 , a5 , 分数在[90,100]内的学生有2人,记这2人分别为b1 , b2 , 列举法易得


科目:高中数学 来源: 题型:
【题目】若a1 , a2 , a3 , …a20这20个数据的平均数为 ![]() ,方差为0.21,则a1 , a2 , a3 , …a20 ,
,方差为0.21,则a1 , a2 , a3 , …a20 , ![]() 这21个数据的方差为( )
这21个数据的方差为( )
A.0.19
B.0.20
C.0.21
D.0.22
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某园艺公司种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了![]() 棵树苗的高度(单位:厘米),并把这些高度列成如下的频数分布表:
棵树苗的高度(单位:厘米),并把这些高度列成如下的频数分布表:
组别 |
|
|
|
|
|
|
频数 | 2 | 4 | 11 | 16 | 13 | 4 |
(Ⅰ)在这批树苗中任取一棵,其高度在![]() 厘米以上的概率大约是多少?这批树苗的平均高度大约是多少?
厘米以上的概率大约是多少?这批树苗的平均高度大约是多少?
(Ⅱ)为了进一步获得研究资料,标记![]() 组中的树苗为
组中的树苗为![]() ,
,![]() 组中的树苗为
组中的树苗为![]() ,现从
,现从![]() 组中移出一棵树苗,从
组中移出一棵树苗,从![]() 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则![]() 组的树苗
组的树苗![]() 和
和![]() 组的树苗
组的树苗![]() 同时被移出的概率是多少?
同时被移出的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在物理实验中,为了研究所挂物体的重量x对弹簧长度y的影响.某学生通过实验测量得到物体的重量与弹簧长度的对比表:
物体重量(单位g) | 1 | 2 | 3 | 4 | 5 |
弹簧长度(单位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
(1)画出散点图;
(2)利用公式(公式见卷首)求y对x的回归直线方程;
(3)预测所挂物体重量为8g时的弹簧长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
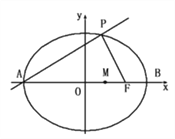
【题目】如图,A、B分别是椭圆![]() 的左、右端点,F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
的左、右端点,F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
(1)点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于MB,求椭圆上的点到点M的距离d的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:(x﹣1)2+(y﹣1)2=4,直线l过点P(2,3)且与圆M交于A,B两点,且|AB|=2 ![]() .
.
(1)求直线l方程;
(2)设Q(x0 , y0)为圆M上的点,求x02+y02的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)关于![]() 的不等式
的不等式![]() 在
在![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)关于![]() 的方程
的方程![]() 有两个实根
有两个实根![]() ,
, ![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com