练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】将圆为参数)上的每一点的横坐标保持不变，纵坐标变为原来的倍，得到曲线

    (1)求出的普通方程；

    (2)设直线： 与的交点为， ，以坐标原点为极点， 轴正半轴为极轴建立极坐标系，求过线段的中点且与垂直的直线的极坐标方程.

    【答案】（1）（2）

    【解析】试题分析：（1）本问首先应用伸缩变换公式，根据公式可以得到变化后的参数方程为（为参数），即，于是可以根据画为普通方程；（2）将曲线的普通方程与直线的方程联立，可以解方程组，方程组的解分别为两点坐标，于是可以求出直线的斜率及中点坐标，根据垂直关系可以求出线段的垂直平分线的方程，然后根据极坐标与直角坐标互化公式，即得到直线的极坐标方程.

    试题解析：(1)设为圆上的任意一点，在已知的变换下变为上的点，

    则有

    (2) 解得：

    所以则线段的中点坐标为，所求直线的斜率，于是所求直线方程为.

    化为极坐标方程得： ，即

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知美国苹果公司生产某款iPhone手机的年固定成本为40万美元，每生产1万只还需另投入16万美元．设苹果公司一年内共生产该款iPhone手机x万只并全部销售完，每万只的销售收入为R(x)万美元，且R(x)＝

    (1)写出年利润W(万美元)关于年产量x(万只)的函数解析式；

    (2)当年产量为多少万只时，苹果公司在该款iPhone手机的生产中所获得的利润最大？并求出最大利润．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知A（3，0），B（0，3）C（cosα，sinα），O为原点．
    （1）若∥ ， 求tanα的值；
    （2）若 ， 求sin2α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四个函数：①y＝3－x；②y＝；③y＝x2＋2x－10；④y＝－.其中值域为R的函数个数有(　　)

    A. 1个 B. 2个

    C. 3个 D. 4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，AA1=AC=2AB=2，且BC1⊥A1C．
    （1）求证：平面ABC1⊥平面A1ACC1；
    （2）设D是线段BB1的中点，求三棱锥D﹣ABC1的体积．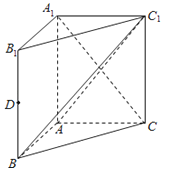

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用二分法研究函数f（x）=x3+3x﹣1的零点时，第一次经计算f（0）＜0，f（0.5）＞0，可得其中一个零点x0∈ ，第二次应计算的f（x）的值为f（ ）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，曲线的参数方程为（， 为参数），在以为极点， 轴的正半轴为极轴的极坐标系中，曲线是圆心在极轴上，且经过极点的圆.已知曲线上的点对应的参数，射线与曲线交于点.

    （Ⅰ）求曲线的直角坐标方程；

    （Ⅱ）若点， 在曲线上，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数f（x）=kax﹣a﹣x（a＞0且a≠1）在（﹣∞，+∞）上既是奇函数又是增函数，则函数g（x）=loga（x+k）的图象是（　　）
    A.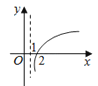
    B.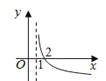
    C.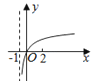
    D.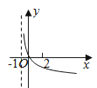

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方体ABCD﹣A1B1C1D1中，M、N分别为棱C1D1、C1C的中点，有以下四个结论：
    ①直线AM与CC1是相交直线；
    ②直线AM与BN是平行直线；
    ③直线BN与MB1是异面直线；
    ④直线AM与DD1是异面直线．
    其中正确的结论为 （注：把你认为正确的结论的序号都填上）．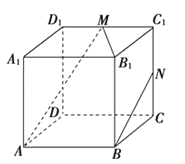

    查看答案和解析>>

    同步练习册答案