Question

11．某研究所计划利用“神七”宇宙飞船进行新产品搭载实验，计划搭载若干件新产品A、B，该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排，通过调查，有关数据如表：

	每件产品A	每件产品B
研制成本、搭载 费用之和（万元）	20	30	计划最大资金额 300万元
产品重量（千克）	10	5	最大搭载重量110千克
预计收益（万元）	80	60

如何安排这两种产品的件数进行搭载，才能使总预计收益达到最大，最大收益是多少？

Answer 1

分析 设搭载的产品中A有x件，产品B有y件，得到关于x，y的不等式组，即约束条件和目标函数，然后根据线行规划的方法不难得到结论．

解答 解：解：设搭载产品Ax件，产品By件，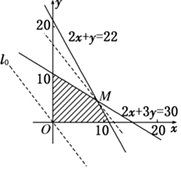
预计总收益z=80x+60y．
则$\left\{\begin{array}{l}{20x+30y≤300}\\{10x+5y≤110}\\{x∈N，y∈N}\end{array}\right.$，作出可行域，如图．
作出直线l₀：4x+3y=0并平移，由图象得，
当直线经过M点时z能取得最大值，
$\left\{\begin{array}{l}{2x+3y=30}\\{2x+y=22}\end{array}\right.$，解得M（9，4）．
∴z_max=80×9+60×4=960（万元）．
答：搭载产品A9件，产品B4件，可使得总预计收益最大，为960万元．

点评 本题考查简单的线性规划，考查简单的数学建模思想方法与数形结合的解题思想方法，是中档题．