
若 =
= ,
, =
= ,其中
,其中 >0,记函数f(x)=2
>0,记函数f(x)=2 ·
· ,f(x)图象中相邻两条对称轴间的距离为
,f(x)图象中相邻两条对称轴间的距离为 ,(1)求
,(1)求 的值;
的值;
(2)求f(x)的单调减区间和f(x)的最大值及取得最大值时x的取值集合.
科目:高中数学 来源:2012-2013学年山东省泰安市高三12月质检文科数学试卷(解析版) 题型:解答题
若 =
= ,
, =
= ,其中
,其中 >0,记函数f(x)=2
>0,记函数f(x)=2 ·
· ,f(x)图象中相邻两条对称轴间的距离为
,f(x)图象中相邻两条对称轴间的距离为 ,
,
(1)求 的值;
的值;
(2)求f(x)的单调减区间和f(x)的最大值及取得最大值时x的取值集合.
查看答案和解析>>
科目:高中数学 来源:新课标高三数学三角函数专项训练(河北) 题型:填空题
下列命题:
①若f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,θ∈,则f(sin θ)>f(cos θ);
②若锐角α,β满足cos α>sin β,则α+β<;
③若f(x)=2cos2-1,则f(x+π)=f(x)对x∈R恒成立;
④要得到函数y=sin的图象,只需将y=sin的图象向右平移个单位,其中真命题是________(把你认为所有正确的命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三第二次月考理科数学卷 题型:解答题
(本小题满分13分)若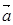 =
=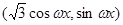 ,
,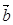 =
=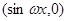 ,其中
,其中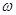 >0,记函数f(x)=(
>0,记函数f(x)=(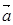 +
+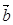 )·
)·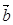 +k.
+k.
(1)若f(x)图象中相邻两条对称轴间的距离不小于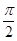 ,求
,求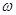 的取值范围.
的取值范围.
(2)若f(x)的最小正周期为 ,且当x
,且当x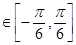 时,f(x)的最大值是
时,f(x)的最大值是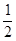 ,求f(x)的解析式,
,求f(x)的解析式,
查看答案和解析>>
科目:高中数学 来源:福建省漳州三中2010-2011学年高三第二次月考数学(文) 题型:解答题
若 =
= ,
, =
= ,其中
,其中 >0,记函数f(x)=2
>0,记函数f(x)=2 ·
· ,f(x)图象中相邻两条对称轴间的距离为
,f(x)图象中相邻两条对称轴间的距离为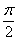 ,(1)求
,(1)求 的值;(2)求f(x)的单调减区间和f(x)的最大值及取得最大值时x的取值集合.
的值;(2)求f(x)的单调减区间和f(x)的最大值及取得最大值时x的取值集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com