
【题目】设函数f(x)=|2x+1|﹣|x﹣4|.
(1)解不等式f(x)>0;
(2)若f(x)+3|x﹣4|>m对一切实数x均成立,求m的取值范围.
【答案】
(1)
解:当x≥4时f(x)=2x+1﹣(x﹣4)=x+5>0得 x>﹣5,所以,x≥4时,不等式成立.
当 ![]() 时,f(x)=2x+1+x﹣4=3x﹣3>0,得x>1,所以,1<x<4时,不等式成立.
时,f(x)=2x+1+x﹣4=3x﹣3>0,得x>1,所以,1<x<4时,不等式成立.
当 ![]() 时,f(x)=﹣x﹣5>0,得x<﹣5,所以,x<﹣5成立
时,f(x)=﹣x﹣5>0,得x<﹣5,所以,x<﹣5成立
综上,原不等式的解集为:{x|x>1或x<﹣5}
(2)
解:f(x)+3|x﹣4|=|2x+1|+2|x﹣4|≥|2x+1﹣(2x﹣8)|=9,当且仅当﹣ ![]() ≤x≤4时,取等号,
≤x≤4时,取等号,
所以,f(x)+3|x﹣4|的最小值为9,故 m<9
【解析】(1)分类讨论,当x≥4时,当 ![]() 时,当
时,当 ![]() 时,分别求出不等式的解集,再把解集取交集.(2)利用绝对值的性质,求出f(x)+3|x﹣4|的最小值为9,故m<9.
时,分别求出不等式的解集,再把解集取交集.(2)利用绝对值的性质,求出f(x)+3|x﹣4|的最小值为9,故m<9.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() :
: 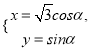 (
(![]() 为参数),在以
为参数),在以![]() 原点为极点,
原点为极点, ![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,求点
两点,求点![]() 到
到![]() ,
, ![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是一个非空集合,
是一个非空集合, ![]() 是定义在
是定义在![]() 上的一个运算.如果同时满足下述四个条件:
上的一个运算.如果同时满足下述四个条件:
(1)对于![]() ,都有
,都有![]() ;
;
(2)对于![]() ,都有
,都有![]() ;
;
(3)对于![]() ,使得
,使得![]() ;
;
(4)对于![]() ,使得
,使得![]() (注:“
(注:“![]() ”同(iii)中的“
”同(iii)中的“![]() ”).
”).
则称![]() 关于运算
关于运算![]() 构成一个群.现给出下列集合和运算:
构成一个群.现给出下列集合和运算:
①![]() 是整数集合,
是整数集合, ![]() 为加法;②
为加法;②![]() 是奇数集合,
是奇数集合, ![]() 为乘法;③
为乘法;③![]() 是平面向量集合,
是平面向量集合, ![]() 为数量积运算;④
为数量积运算;④![]() 是非零复数集合,
是非零复数集合, ![]() 为乘法. 其中
为乘法. 其中![]() 关于运算
关于运算![]() 构成群的序号是___________(将你认为正确的序号都写上).
构成群的序号是___________(将你认为正确的序号都写上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:
女生:
睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
人数 | 2 | 4 | 8 | 4 | 2 |
男生:
睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
人数 | 1 | 5 | 6 | 5 | 3 |
(1)现把睡眠时间不足5小时的定义为“严重睡眠不足”,从睡眠时间不足6小时的女生中随机抽取2人,求此2人中恰有一人为“严重睡眠不足”的概率;
(2)完成下面2×2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”?
睡眠时间少于7小时 | 睡眠时间不少于7小时 | 合计 | |
男生 | |||
女生 | |||
合计 |
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
( ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,角A,B,C的对边分别是a,b,c,向量m=(2b,1),n=(2a-c,cos C),且m∥n.(1)若b2=ac,试判断△ABC的形状;(2)求y=1-![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前n项和为
的前n项和为![]() ,
, ![]() ,
, ![]() ,数列
,数列![]() 满足:
满足: ![]() ,
, ![]() ,
, ![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]()
(1)求数列![]() 的通项公式及前n项和;
的通项公式及前n项和;
(2)求数列![]() 的通项公式及前n项和;
的通项公式及前n项和;
(3)记集合 ,若M的子集个数为16,求实数
,若M的子集个数为16,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 为偶函数
为偶函数
(1)求实数a的值;
(2)记集合E={y|y=f(x),x∈{﹣1,1,2}},λ=lg22+lg2lg5+lg5﹣ ![]() ,判断λ与E的关系;
,判断λ与E的关系;
(3)当x∈[ ![]() ,
, ![]() ](m>0,n>0)时,若函数f(x)的值域[2﹣3m,2﹣3n],求实数m,n值.
](m>0,n>0)时,若函数f(x)的值域[2﹣3m,2﹣3n],求实数m,n值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com