
【题目】在平面直角坐标系中,O为坐标原点,A,B,C三点满足 ![]() =
= ![]() +
+ ![]() . (Ⅰ)求证:A,B,C三点共线;
. (Ⅰ)求证:A,B,C三点共线;
(Ⅱ)已知A(1,cosx),B(1+sinx,cosx),x∈[0, ![]() ],f(x)=
],f(x)= ![]()
![]() ﹣(2m2+
﹣(2m2+ ![]() )|
)| ![]() |的最小值为
|的最小值为 ![]() ,求实数m的值.
,求实数m的值.
科目:高中数学 来源: 题型:
【题目】在棱长都相等的四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,则下面四个结论中不成立的是 ( )
A.BC∥平面PDF
B.DF⊥平面PAE
C.平面PDF⊥平面ABC
D.平面PAE⊥平面ABC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂修建一个长方体形无盖蓄水池,其容积为4800立方米,深度为3米.池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底长方形长为x米.
(Ⅰ)求底面积并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示. 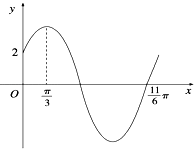
(1)求f(x)的解析式;
(2)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的 ![]() 倍,再将所得函数图象向右平移
倍,再将所得函数图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
(3)当x∈[﹣ ![]() ,
, ![]() ]时,求函数y=f(x+
]时,求函数y=f(x+ ![]() )﹣
)﹣ ![]() f(x+
f(x+ ![]() )的最值.
)的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:x2=2py(p>0),直线y=kx+2与E交于A、B两点,且 ![]() =2,其中O为原点.
=2,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为(0,﹣2),记直线CA、CB的斜率分别为k1 , k2 , 证明:k12+k22﹣2k2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A=[a﹣3,a],函数 ![]() (﹣2≤x≤5)的单调减区间为集合B.
(﹣2≤x≤5)的单调减区间为集合B.
(1)若a=0,求(RA)∪(RB);
(2)若A∩B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位要在800名员工中抽去80名员工调查职工身体健康状况,其中青年员工400名,中年员工300名,老年员工100名,下列说法错误的是( )
A.老年人应作为重点调查对象,故抽取的老年人应超过40名
B.每个人被抽到的概率相同为 ![]()
C.应使用分层抽样抽取样本调查
D.抽出的样本能在一定程度上反映总体的健康状况
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,平面内有三个向量 ![]() ,
, ![]() ,
, ![]() ,其中
,其中 ![]() 与
与 ![]() 的夹角为30°,
的夹角为30°, ![]() 与
与 ![]() 的夹角为90°,且|
的夹角为90°,且| ![]() |=2,|
|=2,| ![]() |=2,|
|=2,| ![]() |=2
|=2 ![]() ,若
,若 ![]() =λ
=λ ![]() +μ
+μ ![]() ,(λ,μ∈R)则( )
,(λ,μ∈R)则( ) 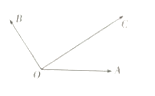
A.λ=4,μ=2
B.λ=4,μ=1
C.λ=2,μ=1
D.λ=2,μ=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com