
已知椭圆C: 的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=
的两个焦点为F1、F2,点P在椭圆C上,且|PF1|= ,
,
|PF2|= , PF1⊥F1F2.
, PF1⊥F1F2.
(1)求椭圆C的方程;(6分)
(2)若直线L过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程.
(1)椭圆C的方程为 =1. (2)所求的直线方程为8x-9y+25=0.
=1. (2)所求的直线方程为8x-9y+25=0.
【解析】
试题分析:(1) ∵点P在椭圆C上,∴ ,a=3.
,a=3.
在Rt△PF1F2中, 故椭圆的半焦距c=
故椭圆的半焦距c= ,
,
从而b2=a2-c2="4," ∴椭圆C的方程为 =1.
=1.
(2)设A,B的坐标分别为(x1, y1)、(x2, y2). ∵圆的方程为(x+2)2+(y-1)2=5, ∴圆心M的坐标为(-2,1). 从而可设直线l的方程为 y="k(x+2)+1," 代入椭圆C的方程得
(4+9k2)x2+(36k2+18k)x+36k2+36k-27=0. (*)
又∵A、B关于点M对称. ∴ 解得
解得 ,
,
∴直线l的方程为 即8x-9y+25=0. 此时方程(*)的
即8x-9y+25=0. 此时方程(*)的
 ,故所求的直线方程为8x-9y+25=0.
,故所求的直线方程为8x-9y+25=0.
解法二:(1)同解法一.
(2)已知圆的方程为(x+2)2+(y-1)2=5, ∴圆心M的坐标为(-2,1).
设A,B的坐标分别为(x1,y1),(x2,y2). 由题意x1 x2且
x2且
 ①
①
 ②
②
由①-②得  ③
③
又∵A、B关于点M对称,∴x1+ x2=-4, y1+ y2=2, 代入③得 =
= ,即直线l的斜率为
,即直线l的斜率为 ,
,
∴直线l的方程为y-1= (x+2),即8x-9y+25="0." 此时方程(*)的
(x+2),即8x-9y+25="0." 此时方程(*)的  ,故所求的直线方程为8x-9y+25=0.
,故所求的直线方程为8x-9y+25=0.
考点:本题主要考查椭圆的标准方程,直线与圆、椭圆的位置关系。
点评:中档题,本题求椭圆的标准方程时,应用了椭圆的定义。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本解法给出了两种思路,其中思路1主要是利用韦达定理,结合对称性求得直线方程;思路2则利用了“点差法”求斜率,进一步结合对称性求得直线方程。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:| y2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| PA |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省湛江二中高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的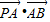 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.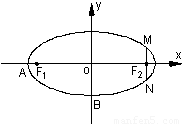
查看答案和解析>>
科目:高中数学 来源:2010年内蒙古赤峰市高三统考数学试卷(文科)(解析版) 题型:解答题
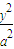 +
+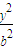 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=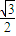 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的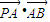 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.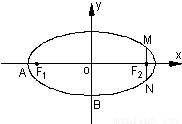
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com