
分析 由题意首先求出M的轨迹方程,然后在M满足的曲线上设点,只要求曲线上到圆心的距离的最小值,即可得到|ST|的最小值.
解答 解:设M坐标为 M(x,y),由MP⊥l知 P(-$\frac{1}{2}$,y),
由点Q为PF的中点知 Q(0,$\frac{y}{2}$),
又因为QM⊥PF,QM、PF斜率乘积为-1,即 $\frac{y-\frac{y}{2}}{x}$=-$\frac{-\frac{1}{2}-\frac{1}{2}}{y}$,
解得:y2=2x,
∴M的轨迹是抛物线,
设M(y2,$\sqrt{2}$y),到圆心(3,0)的距离为d,d2=(y2-3)2+2y2=y4-4y2+9=(y2-2)2+5,
∴y2=2时,dmin=$\sqrt{5}$,此时的切线长为$\sqrt{5-2}=\sqrt{3}$,
∴|ST|的最小值为2×$\frac{\sqrt{3}×\sqrt{2}}{\sqrt{5}}$=$\frac{2\sqrt{30}}{5}$.
故答案为:$\frac{2\sqrt{30}}{5}$.
点评 本题考查了抛物线轨迹方程的求法以及与圆相关的距离的最小值求法,属于中档题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
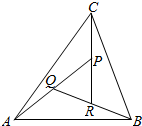 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )| A. | $\frac{2}{7},\frac{4}{7}$ | B. | $\frac{1}{2},\frac{1}{4}$ | C. | $\frac{1}{6},\frac{2}{7}$ | D. | $\frac{1}{6},\frac{3}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{4\sqrt{65}}{65}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com