
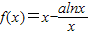 ,其中a为常数.
,其中a为常数.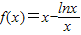 ,
,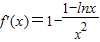 ,即
,即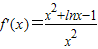 ,
,| x | (0,1) | 1 | (1,+∞) |
| f'(x) | - | + | |
| f(x) | 极小值 |
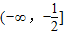 .…(9分)
.…(9分)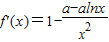 ,即
,即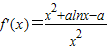 ,令h(x)=x2+alnx-a,
,令h(x)=x2+alnx-a,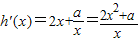 ,令h'(x)=0,得
,令h'(x)=0,得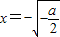 (舍)或
(舍)或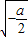 .
.| x | (0,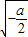 ) ) | 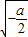 | (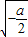 ,+∞) ,+∞) |
| h'(x) | - | + | |
| h(x) | ↘ | 极小值 | ↗ |
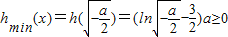 ,解得a≥-2e3.
,解得a≥-2e3.

科目:高中数学 来源: 题型:
(08年崇文区统一练习一)(14分)
已知定义在R上的函数![]() ,其中a为常数.
,其中a为常数.
(I)若x=1是函数![]() 的一个极值点,求a的值;
的一个极值点,求a的值;
(II)若函数![]() 在区间(-1,0)上是增函数,求a的取值范围;
在区间(-1,0)上是增函数,求a的取值范围;
(III)若函数![]() ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省揭阳市普宁市普师高级中学高三(上)摸底数学试卷(理科)(解析版) 题型:解答题
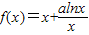 ,其中a为常数.
,其中a为常数.查看答案和解析>>
科目:高中数学 来源:2010年广东省湛江市高考数学一模试卷(文科)(解析版) 题型:解答题
 ,其中a为常数.
,其中a为常数.查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京四中高三上学期期中考试数学文卷 题型:解答题
(本小题满分13分)已知:定义在R上的函数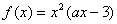 ,其中a为常数。
,其中a为常数。
(1)若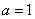 ,求:
,求: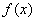 的图象在点
的图象在点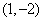 处的切线方程;
处的切线方程;
(2)若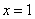 是函数
是函数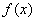 的一个极值点,求:实数a的值;
的一个极值点,求:实数a的值;
(3)若函数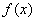 在区间
在区间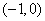 上是增函数,求:实数a的取值范围。
上是增函数,求:实数a的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com