练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．用红、黄、蓝三种颜色对如图所示的三个方格进行涂色．若要求每个小方格涂一种颜色，且涂成红色的方格数为偶数，则不同的涂色方案种数是14．（用数字作答）

    分析 由题意可知涂成红色的方格数为0，或2，分三类，3个格涂一种颜色，3个格涂2颜色且涂0个红色时，3格涂2颜色且涂2个红色时，根据分类计数原理可得．

    解答 解：因为涂成红色的方格数为偶数，即涂成红色的方格数为0，或2，
    3个格涂一种颜色，有2种，（全黄或全蓝）
    3个格涂2颜色且涂0个红色时，C21C32=6种，
    3格涂2颜色且涂2个红色时，C21C32=6种，
    根据分类计数原理，可得共有2+6+6=14种，
    故答案为：14．

    点评 本题考查了分类计数原理，关键是分类，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．已知函数f（x）=10-x-|lgx|与x轴有两个交点（x1，0），（x2，0），则（　　）
    A．0＜x1x2＜1B．x1x2=1C．-1＜x1x2＜0D．1＜x1x2＜10

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．方程x2+x+n=0（n∈[0，1]）有实根的概率为$\frac{1}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

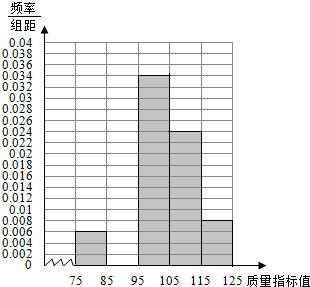    17．从某企业生茶的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量结果得如下频数分布表：
    质量指标值分组[75，85）[85，95）[95，105）[105，115）[115，125）
    频数62834248
    （1）在答题卡上补全这些数据作出的频率分布直方图；
    （2）估计这种产品质量指标值的平均值及方差（同一组中的数据用该组区间的中点值作代表）；
    （3）估计这种产品质量指标值的中位数．（精确到0.1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．设a=0.23，b=log20.3，c=20.3，则（　　）
    A．b＜c＜aB．c＜b＜aC．a＜b＜cD．b＜a＜c

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．如图表示的是求首项为-41，公差为2的等差数列{an}前n项和的最小值的程序框图．则①处可填写（　　）
    A．S＞0B．S＜0C．a＞0D．a=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=alnx-x+2，其中a≠0．
    （Ⅰ）求f（x）的单调区间；
    （Ⅱ）若对任意的x1∈[1，e]，总存在x2∈[1，e]，使得f（x1）+f（x2）=4，求实数a值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．从某小学随机抽取100名学生，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）．

    （1）由图中数据求a．
    （2）由图估计样本的众数、中位数、平均数． （说明理由）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．将正整数按下表排列：
    第1列第2列第3列第4列
    第1行1234
    第2行8765
    第3行9101112
    第4行16151413
    ……………
    则101在（　　）
    A．第25行，第1列B．第25行，第4列C．第26行，第1列D．第26行，第4列

    查看答案和解析>>

    同步练习册答案