练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某单位决定投资3200元建一仓库(长方体状)，高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米长造价40元，两侧墙砌砖，每米造价45元，顶部每平方米造价20元，试算:仓库底面积S的最大允许值是多少？此时铁栅长为多少？

    设铁栅长x m，一堵墙长y m，则有S=xy.

    由题意得40x+2×45y+20xy=3200.

    应用二元均值不等式，得3200≥2+20xy=120+20xy=120+20S.

    ∴S+6≤160.

    ∴(－10)(+16)≤0.

    由于+16＞0,∴－10≤0，即S≤100.

    因此S的最大允许值是100 m2，当且仅当40x=90y,

    而xy=100,解得x=15，

    即铁栅的长应为15 m.


    解析:

    本题考查不等式在实际中的应用.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某单位决定投资3200元建一仓库（长方体状），高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米长造价40元，两侧墙砌砖，每米造价45元，屋顶每平方米造价20元，试计算：
    （1）仓库面积S的最大允许值是多少？
    （2）为使S达到最大，而实际投资又不超过预算，那么正面铁栅应设计为多长？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某单位决定投资3200元建一仓库（长方体状），高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米长造价40元，两侧墙砌砖，每米造价45元，屋顶每平方米造价20元，试计算：仓库面积S的最大允许值为多少？

    查看答案和解析>>

    科目：高中数学 来源：2015届湖北省高一下学期期中联考文科数学试卷（解析版） 题型：解答题

    某单位决定投资3200元建一仓库（长方体状），高度恒定，它的后墙利用旧墙，地面利用原地面均不花钱，正面用铁栅，每米长造价40元，两侧墙砌砖，每米长造价45元，屋顶每平方米造价20元．

    （1）仓库面积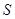的最大允许值是多少？

    （2）为使面积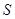达到最大而实际投入又不超过预算，正面铁栅应设计为多长？

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省聊城外国语学校高三（上）第三次月考数学试卷（文科）（解析版） 题型：解答题

    某单位决定投资3200元建一仓库（长方体状），高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米长造价40元，两侧墙砌砖，每米造价45元，屋顶每平方米造价20元，试计算：
    （1）仓库面积S的最大允许值是多少？
    （2）为使S达到最大，而实际投资又不超过预算，那么正面铁栅应设计为多长？

    查看答案和解析>>

    同步练习册答案