
【题目】图,从甲地到丙地要经过两个十字路口(十字路口![]() 与十字路口
与十字路口![]() ),从乙地到丙地也要经过两个十字路口(十字路口
),从乙地到丙地也要经过两个十字路口(十字路口![]() 与十字路口
与十字路口![]() ),设各路口信号灯工作相互独立,且在
),设各路口信号灯工作相互独立,且在![]() ,
,![]() ,
,![]() ,
,![]() 路口遇到红灯的概率分别为
路口遇到红灯的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求一辆车从乙地到丙地至少遇到一个红灯的概率;
(2)若小方驾驶一辆车从甲地出发,小张驾驶一辆车从乙地出发,他们相约在丙地见面,记![]() 表示这两人见面之前车辆行驶路上遇到的红灯的总个数,求
表示这两人见面之前车辆行驶路上遇到的红灯的总个数,求![]() 的分布列及数学期望.
的分布列及数学期望.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 ![]() (t为参数),圆C的参数方程为
(t为参数),圆C的参数方程为 ![]() (θ为常数).
(θ为常数).
(1)求直线l和圆C的普通方程;
(2)若直线l与圆C有公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的有______
①平均数不受少数几个极端值的影响,中位数受样本中的每一个数据影响;
②抛掷两枚硬币,出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大
③用样本的频率分布估计总体分布的过程中,样本容量越大,估计越准确.
④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在x轴正半轴上,半径为5,且与直线![]() 相切.
相切.
(1)求圆C的方程;
(2)设点![]() ,过点
,过点![]() 作直线
作直线![]() 与圆C交于
与圆C交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)设P是直线![]() 上的点,过P点作圆C的切线
上的点,过P点作圆C的切线![]() ,切点为
,切点为![]() 求证:经过
求证:经过![]() 三点的圆必过定点,并求出所有定点的坐标.
三点的圆必过定点,并求出所有定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个不相等的非零向量 ![]() ,
, ![]() ,两组向量
,两组向量 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 和
和 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 均由2个
均由2个 ![]() 和3个
和3个 ![]() 排列而成,记S=
排列而成,记S= ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() ,Smin表示S所有可能取值中的最小值.则下列命题正确的是(写出所有正确命题的编号).
,Smin表示S所有可能取值中的最小值.则下列命题正确的是(写出所有正确命题的编号).
①S有5个不同的值;
②若 ![]() ⊥
⊥ ![]() ,则Smin与|
,则Smin与| |无关;
③若 ![]() ∥
∥ ![]() ,则Smin与|
,则Smin与| ![]() |无关;
|无关;
④若| ![]() |>4|
|>4| ![]() |,则Smin>0;
|,则Smin>0;
⑤若| ![]() |=2|
|=2| ![]() |,Smin=8|
|,Smin=8| ![]() |2 , 则
|2 , 则 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生的课外阅读时间情况,某学校随机抽取了50人进行统计分析,把这50人每天阅读的时间(单位:分钟)绘制成频数分布表,如下表所示:
阅读时间 |
|
|
|
|
|
|
人数 | 8 | 10 | 12 | 11 | 7 | 2 |
若把每天阅读时间在60分钟以上(含60分钟)的同学称为“阅读达人”,根据统计结果中男女生阅读达人的数据,制作成如图所示的等高条形图.
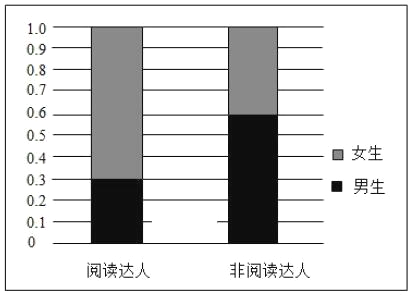
(1)根据抽样结果估计该校学生的每天平均阅读时间(同一组数据用该区间的终点值作为代表);
(2)根据已知条件完成下面的![]() 列联表,并判断是否有99%的把握认为“阅读达人”跟性别有关?
列联表,并判断是否有99%的把握认为“阅读达人”跟性别有关?
男生 | 女生 | 总计 | |
阅读达人 | |||
非阅读达人 | |||
总计 |
附:参考公式![]() ,其中
,其中![]() .
.
临界值表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查观众对电视剧《风筝》的喜爱程度,某电视台举办了一次现场调查活动.在参加此活动的甲、乙两地大量观众中,各随机抽取了8名观众对该电视剧评分做调查(满分100分),被抽取的观众的评分结果如图所示.

(1)从甲地抽取的8名观众和乙地抽取的8名观众中分别各选取一人,在已知两人中至少一人评分不低于90分的条件下,求乙地被选取的观众评分低于90分的概率。
(2)从甲地抽取出来的8名观众中选取1人,从乙地抽取出来的8名观众中选取2人去参加代表大会,记选取的3人中评分不低于90分的人数为![]() ,求
,求![]() 的分布列与期望。
的分布列与期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com