
【题目】杨辉三角是二项式系数在三角形中的一种排列,在欧洲这个表叫做帕斯卡三角形,帕斯卡是在1654年发现这一规律的,我国南宋数学家杨辉在1261年所著的《详解九章算法》一书中出现了如图所示的表,这是我国数学史上的一次伟大成就,如图所示,在“杨辉三角”中去除所有为1的项,依次构成数列,2,3,3,4,6,4,5 ,10 ,10,5,……,则此数列的前119项的和为__________.(参考数据:![]() ,
,![]() ,
,![]() )
)

【答案】131022
【解析】
分析“杨辉三角形”的性质,每一行的数字和为首项为1,公比为2的等比数列,除去1之后各行的项的个数为首项为1,公差为1的等差数列,其中所求数列的前119项可以视为,杨辉三角形中前17行中除去1和第17行的最后一个数之外的项之和,分别计算即可.
n次二项系数对应杨辉三角的第n+1行,例如![]() ,系数分别为1,2,1,对应杨辉三角的第三行,令x=1,就可以求出该行的系数之和,
,系数分别为1,2,1,对应杨辉三角的第三行,令x=1,就可以求出该行的系数之和,
第1行为![]() ,第2行为
,第2行为![]() ,第3行为
,第3行为![]() ,以此类推即每一行数字和为首项为1,公比为2的等比数列,则杨辉三角形的前n项和为
,以此类推即每一行数字和为首项为1,公比为2的等比数列,则杨辉三角形的前n项和为![]() ,
,
若去除所有的为1的项,则剩下的每一行的个数为1,2,3,4,……,可以看成构成一个首项为1,公差为1的等差数列,则前n项和![]() ,
,
可得当n=14,再加上第15行的前14项时,所有项的个数和为119,
由于最右侧为2,3,4,5,……,为一个首项为2,公差为1的等差数列,则第15行的第15项为16,
则杨辉三角的前17项和为![]() ,且前17行中有
,且前17行中有![]() 个1,
个1,
故此数列的前119项的和为![]() .
.
故答案为:131022


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 表示不超过
表示不超过![]() 的最大整数,下列关于
的最大整数,下列关于![]() 说法正确的有:______.
说法正确的有:______.
①![]() 的值域为[-1,1]
的值域为[-1,1]
②![]() 为奇函数
为奇函数
③![]() 为周期函数,且最小正周期T=4
为周期函数,且最小正周期T=4
④![]() 在[0,2)上为单调增函数
在[0,2)上为单调增函数
⑤![]() 与
与![]() 的图像有且仅有两个公共点
的图像有且仅有两个公共点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如图:

每名快递员完成一件货物投递可获得的劳务费情况如下:甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;
(2)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为X(单位:元),求X的分布列和数学期望;
(3)根据表中数据估算两公司的每位员工在该月所得的劳务费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的有( )
①常数数列既是等差数列也是等比数列;②在![]() 中,若
中,若![]() ,则
,则![]() 为直角三角形;③若
为直角三角形;③若![]() 为锐角三角形的两个内角,则
为锐角三角形的两个内角,则![]() ;④若
;④若![]() 为数列
为数列![]() 的前
的前![]() 项和,则此数列的通项
项和,则此数列的通项![]() .
.
A.①②B.②③C.③④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,点
,点![]() 为线段AB的中点,设点
为线段AB的中点,设点![]() 的轨迹为
的轨迹为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知直线![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() ,若直线
,若直线![]() 的斜率之和为3,直线
的斜率之和为3,直线![]() 是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() ,其中
,其中![]() ;
;
(1)试求不等式的解集![]() ;
;
(2)对于不等式的解集![]() ,记
,记![]() (其中
(其中![]() 为整数集),若集合
为整数集),若集合![]() 为有限集,求实数
为有限集,求实数![]() 的取值范围,使得集合
的取值范围,使得集合![]() 中元素个数最少,并用列举法表示集合
中元素个数最少,并用列举法表示集合![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
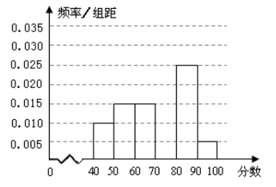
(1)求分数![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com