
在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,P为DN的中点.

(1)求证:BD⊥MC;
(2)线段AB上是否存在点E,使得AP∥平面NEC?若存在,说明在什么位置,并加以证明;若不存在,说明理由.
(1)见解析(2)E为AB的中点时,有AP∥平面NEC
【解析】(1)证明:联结AC,因为四边形ABCD是菱形,
所以AC⊥BD.
又四边形ADNM是矩形,平面ADNM⊥平面ABCD,平面ADNM∩平面ABCD=AD,AM⊥AD,所以AM⊥平面ABCD.
因为BD平面ABCD,所以AM⊥BD.
因为AC∩AM=A,所以BD⊥平面MAC.
又MC平面MAC,所以BD⊥MC.
(2)当E为AB的中点时,有AP∥平面NEC.
取NC的中点S,联结PS,SE.

因为PS∥DC∥AE,PS=AE=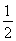 DC,
DC,
所以四边形APSE是平行四边形,所以AP∥SE.
又SE?平面NEC,AP?平面NEC,所以AP∥平面NEC.


科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集17讲练习卷(解析版) 题型:选择题
某社区对该区所辖的老年人是否需要特殊照顾进行了一项分性别的抽样调查,针对男性老年人和女性老年人需要特殊照顾和不需要特殊照顾得出了一个2×2的列联表,并计算得出k=4.350,则下列结论正确的是( )
A.有95%的把握认为该社区的老年人是否需要特殊照顾与性别有关
B.有95%的把握认为该社区的老年人是否需要特殊照顾与性别无关
C.该社区需要特殊照顾的老年人中有95%是男性
D.该地区每100名老年人中有5个需要特殊照顾
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集14讲练习卷(解析版) 题型:填空题
设F1,F2为双曲线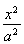 -y2=1的两个焦点,已知点P在此双曲线上,且
-y2=1的两个焦点,已知点P在此双曲线上,且 ·
·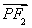 =0.若此双曲线的离心率等于
=0.若此双曲线的离心率等于 ,则点P到x轴的距离等于________.
,则点P到x轴的距离等于________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集13讲练习卷(解析版) 题型:填空题
直线x-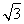 y+2=0被圆x2+y2=4截得的劣弧长为________.
y+2=0被圆x2+y2=4截得的劣弧长为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集13讲练习卷(解析版) 题型:选择题
已知圆C:x2+y2=2与直线l:x+y+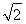 =0,则圆C被直线l所截得的弦长为( )
=0,则圆C被直线l所截得的弦长为( )
A.1 B.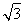 C.2 D.2
C.2 D.2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集12讲练习卷(解析版) 题型:选择题
设m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列为真命题的是( )
A.若α⊥β,m⊥α,则m∥β B.若α⊥γ,β⊥γ,则α∥β
C.若m⊥α,n∥m,则n⊥α D.若m∥α,n∥α,则m∥n
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集11讲练习卷(解析版) 题型:填空题
如图所示的是一几何体的三视图,则该几何体的体积是________.
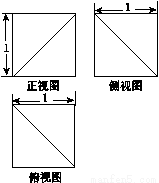
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集10讲练习卷(解析版) 题型:填空题
已知数列{an},an+1=an+2,a1=1,数列 的前n项和为
的前n项和为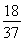 ,则n=________.
,则n=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-4坐标系与参数方程练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,若直线l1: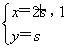 (s为参数)和直线l2:
(s为参数)和直线l2: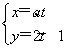 (t为参数)平行,则常数a的值为________.
(t为参数)平行,则常数a的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com