
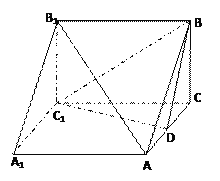
【题目】如图,三棱柱![]() 中,
中,![]() ⊥面
⊥面![]() ,
,![]() ,
,
![]() ,D为AC的中点.
,D为AC的中点.
(Ⅰ)求证:![]() 面BD
面BD![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
(Ⅰ)连接B1C,与BC1相交于O,连接OD.根据三角形的中位线定理判定线面平行。
(Ⅱ)建立空间直角坐标系,求得面BDC1的一个法向量和面ABC的一个法向量,利用法向量求面面夹角,并判断二面角的大小。
(I)证明:连接B1C,与BC1相交于O,连接OD.
∵BCC1B1是矩形,∴O是B1C的中点.
又D是AC的中点,∴OD//AB1. ∵AB1![]() 面BDC1,OD
面BDC1,OD![]() 面BDC1,∴AB1//面BDC1.
面BDC1,∴AB1//面BDC1.

(II)解:如图,建立空间直角坐标系,
则C1(0,0,0),B(0,3,2),
C(0,3,0),A(2,3,0)D(1,3,0),
![]() ,
,![]() ,
,
设![]() 是面BDC1的一个法向量,则
是面BDC1的一个法向量,则
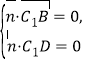 即
即![]() ,取
,取![]() .
.
易知![]() 是面ABC的一个法向量.
是面ABC的一个法向量.
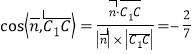 . ∴二面角C1—BD—C的余弦值为
. ∴二面角C1—BD—C的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,顶部每平方米造价20元。
(1)设铁栅长为![]() 米,一堵砖墙长为
米,一堵砖墙长为![]() 米,求函数
米,求函数![]() 的解析式;
的解析式;
(2)为使仓库总面积![]() 达到最大,正面铁栅应设计为多长?
达到最大,正面铁栅应设计为多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={x|9x﹣43x+1+27=0},N={x|log2(x+1)+log2x=log26},则M、N的关系是( )
A.MN
B.NM
C.M=N
D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 其中P,M是非空数集,且P∩M=,设f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.
其中P,M是非空数集,且P∩M=,设f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.
(I)若P=(﹣∞,0),M=[0,4],求f(P)∪f(M);
(II)是否存在实数a>﹣3,使得P∪M=[﹣3,a],且f(P)∪f(M)=[﹣3,2a﹣3]?若存在,请求出满足条件的实数a;若不存在,请说明理由;
(III)若P∪M=R,且0∈M,I∈P,f(x)是单调递增函数,求集合P,M.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( ).
A. ![]() ,“
,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
B. “![]() 且
且![]() 为真命题”是“
为真命题”是“![]() 或
或![]() 为真命题” 的必要不充分条件
为真命题” 的必要不充分条件
C. 命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ”
”
D. 命题![]() :“
:“![]() ”,则
”,则![]() 是真命题
是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是递增数列,且对
是递增数列,且对![]() ,都有
,都有![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由{an}是递增数列,得到an+1>an,再由“an=n2+λn恒成立”转化为“λ>﹣2n﹣1对于n∈N*恒成立”求解.
∵{an}是递增数列,
∴an+1>an,
∵an=n2+λn恒成立
即(n+1)2+λ(n+1)>n2+λn,
∴λ>﹣2n﹣1对于n∈N*恒成立.
而﹣2n﹣1在n=1时取得最大值﹣3,
∴λ>﹣3,
故选:D.
【点睛】
本题主要考查由数列的单调性来构造不等式,解决恒成立问题.研究数列单调性的方法有:比较相邻两项间的关系,将an+1和an做差与0比较,即可得到数列的单调性;研究数列通项即数列表达式的单调性.
【题型】单选题
【结束】
13
【题目】已知数列{an}满足a1=1,且an=an-1+2n![]() 1 (n≥2 ),则a20=________.
1 (n≥2 ),则a20=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x),满足  ,且f(3)=f(1)﹣1.
,且f(3)=f(1)﹣1.
(1)求实数k的值;
(2)若函数g(x)=f(x)+f(﹣x)(﹣2≤x≤2),求g(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com