
分析 (1)利用两个函数有交点,通过判别式列出关系式即可.
(2)直接利用单调性的定义,证明函数在x<0与x>0时都是减函数.得到单调区间.
(3)利用二次函数的性质与一次函数的性质,列出不等式组借助(1)(2)的结论求解即可.
解答 解:(1)实数x为两函数f(x)=x2+mx+2(其中m∈R)与g(x)=x+3图象交点的横坐标.
可得x2+mx+2=x+3.解得m=$-x+\frac{1}{x}+1$.
(2)设x1,x2∈(0,+∞)且x1<x2,
m(x1)-m(x2)=$-{x}_{1}+\frac{1}{{x}_{1}}+1$+${x}_{2}-\frac{1}{{x}_{2}}-1$=x2-x1+$\frac{{x}_{2}-{x}_{1}}{{x}_{1}{x}_{2}}$=(x2-x1)(1+$\frac{1}{{x}_{1}{x}_{2}}$)>0,
可得m(x1)>m(x2),函数是减函数.
x1,x2∈(-∞,0)且x1<x2,
m(x1)-m(x2)=$-{x}_{1}+\frac{1}{{x}_{1}}+1$+${x}_{2}-\frac{1}{{x}_{2}}-1$=x2-x1+$\frac{{x}_{2}-{x}_{1}}{{x}_{1}{x}_{2}}$=(x2-x1)(1+$\frac{1}{{x}_{1}{x}_{2}}$)>0,
可得m(x1)>m(x2),函数是减函数.
函数的单调减区间为:(-∞,0),(0,+∞).
(3)对任意的实数x∈[1,+∞).函数y=f(x)图象恒在y=g(x)的图象上方,
就是x2+mx+2≥x+3.在x∈[1,+∞)恒成立.即m≥$-x+\frac{1}{x}+1$,在x∈[1,+∞)恒成立.
只需m≥($-x+\frac{1}{x}+1$)max,x∈[1,+∞),由(2)可知y=$-x+\frac{1}{x}+1$在x∈[1,+∞)的单调减函数,
可得($-x+\frac{1}{x}+1$)max=1,
∴m≥1.
点评 本题考查函数与方程的综合应用,二次函数的性质以及函数的单调性的应用,函数的最值,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
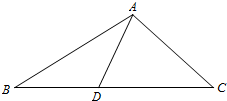 如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )
如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{6}$ | D. | $\frac{\sqrt{3}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=1 | B. | x=-1 | C. | y=1 | D. | y=-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com