
分析 (Ⅰ)抛物线的定义直接求|FA|+|FB|的值(用t表示);
(Ⅱ)设A(x1,y1),B(x2,y2),通过平方差法,求出直线AB的方程,利用弦长公式求|AB|的表达式,然后求解最大值(用t表示).
解答 解:(Ⅰ) 设A(x1,y1),B(x2,y2),M(t,m),则x1+x2=2t,y1+y2=2m.
由抛物线定义知:|FA|=x1+1,|FB|=x2+1.
所以|FA|+|FB|=x1+x2+2=2t+2. …(6分)
(Ⅱ) 由 $\left\{\begin{array}{l}{y_1}^2=4{x_1}\\{y_2}^2=4{x_2}\end{array}\right.$得 (y1+y2) (y1-y2)=4(x1-x2),所以$\frac{{{x_1}-{x_2}}}{{{y_1}-{y_2}}}$=$\frac{m}{2}$.故可设直线AB方程为$\frac{m}{2}$(y-m)=x-t,即x=$\frac{m}{2}$y-$\frac{m^2}{2}$+t.
联立$\left\{\begin{array}{l}x=\frac{m}{2}y-\frac{m^2}{2}+t\\{y^2}=4x\end{array}\right.$消去x,得y2-2my+2m2-4t=0.
则△=16t-4m2>0,y1+y2=2m,y1y2=2m2-4t.所以
|AB|=$\sqrt{1+\frac{m^2}{4}}$|y1-y2|=$\sqrt{(4t-{m^2})(4+{m^2})}$=$\sqrt{-{{[{m^2}-2(t-1)]}^2}+4{{(t+1)}^2}}$,
其中0≤m2<4t.
当t≥1时,因为0≤2t-2<4t,所以,当m2=2t-2时,|AB|取最大值
|AB|max=2t+2.
当0<t<1时,因为2t-2<0,所以,当m2=0时,|AB|取最大值
|AB|max=4$\sqrt{t}$.
综上,|AB|max=$\left\{\begin{array}{l}2t+2,\;\;\;\;t≥1\\ 4\sqrt{t}.\;\;\;\;\;0<t<1\end{array}\right.$
点评 本题考查直线与抛物线位置关系的综合应用,考查分析问题解决问题的能力.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知PBD是⊙O的割线,PA、PC是⊙O的切线,A、C为切点,求证:
如图所示,已知PBD是⊙O的割线,PA、PC是⊙O的切线,A、C为切点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
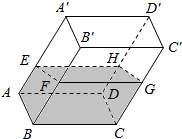 如图,在透明塑料制成的长方体ABCD-A′B′C′D′容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
如图,在透明塑料制成的长方体ABCD-A′B′C′D′容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,⊙O的半径OC垂直于直径AB,M为OB上一点,CM的延长线交⊙O于N,过N点的切线交AB的延长线于P.
如图,⊙O的半径OC垂直于直径AB,M为OB上一点,CM的延长线交⊙O于N,过N点的切线交AB的延长线于P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设A(x0,y0)(x0,y0≠0)是椭圆T:$\frac{{x}^{2}}{m+1}$+y2=1(m>0)上一点,它关于y轴、原点、x轴的对称点依次为B,C,D.E是椭圆T上不同于A的另外一点,且AE⊥AC,如图所示.
设A(x0,y0)(x0,y0≠0)是椭圆T:$\frac{{x}^{2}}{m+1}$+y2=1(m>0)上一点,它关于y轴、原点、x轴的对称点依次为B,C,D.E是椭圆T上不同于A的另外一点,且AE⊥AC,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
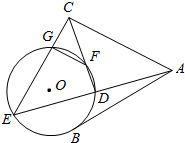 如图,AB是⊙O的一条切线,切点为B,ADE,CFD和 CGE都是⊙O的割线,AC=AB
如图,AB是⊙O的一条切线,切点为B,ADE,CFD和 CGE都是⊙O的割线,AC=AB查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com