
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).设
为参数).设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时,![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的普通方程;
的普通方程;
(2)设![]() 为圆
为圆![]() 上任意一点,求
上任意一点,求![]() 的最大值.
的最大值.
【答案】(1)![]() (
(![]() );(2)
);(2)![]() .
.
【解析】
(1)消元法消去参数![]() 得
得![]() 的普通方程,同理表示
的普通方程,同理表示![]() 的普通方程,最后将其消去
的普通方程,最后将其消去![]() 整理后可得答案;
整理后可得答案;
(2)由椭圆的参数方程表示其上任意点的坐标,由两点间的距离公式表示![]() ,再由三角函数求的值域确定最大值,最后开方即可.
,再由三角函数求的值域确定最大值,最后开方即可.
解法一:(1)消去参数![]() 得
得![]() 的普通方程为
的普通方程为![]() ,
,
消去参数![]() 得
得![]() 的普通方程为
的普通方程为![]() .
.
联立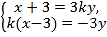 消去
消去![]() 得
得![]() ,
,
所以![]() 的普通方程为
的普通方程为![]() (
(![]() ).
).
(2)依题意,圆心![]() 的坐标为
的坐标为![]() ,半径
,半径![]() .
.
由(1)可知,![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,且
为参数,且![]() ),
),
设![]() (
(![]() ),则
),则
![]()
![]()
![]() ,
,
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
又![]() ,当且仅当
,当且仅当![]() 三点共线,且
三点共线,且![]() 在线段
在线段![]() 上时,等号成立.
上时,等号成立.
所以![]() .
.
解法二:(1)消去参数![]() 得
得![]() 的普通方程为
的普通方程为![]() ,
,
消去参数![]() 得
得![]() 的普通方程为
的普通方程为![]() .
.
由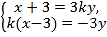 得
得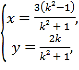
故![]() 的轨迹
的轨迹![]() 的参数方程为
的参数方程为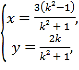 (
(![]() 为参数),
为参数),
所以![]() 的普通方程为
的普通方程为![]() (
(![]() ).
).
(2)同解法一.


科目:高中数学 来源: 题型:
【题目】某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例,以下四个选项错误的是( )



A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少
C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 和圆
和圆![]() :
:![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,当直线
上,当直线![]() 与圆
与圆![]() 相切时,
相切时,![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,且与椭圆
,且与椭圆![]() 和圆
和圆![]() 都相切,切点分别为
都相切,切点分别为![]() ,
,![]() ,记
,记![]() 和
和![]() 的积分别为
的积分别为![]() 和
和![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x22(a+2)x+a2,g(x)=x2+2(a2)xa2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则AB=( )
A.a22a16B.a2+2a16
C.16D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
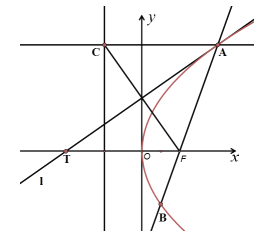
【题目】已知线段![]() 是过抛物线
是过抛物线![]() 的焦点F的一条弦,过点A(A在第一象限内)作直线
的焦点F的一条弦,过点A(A在第一象限内)作直线![]() 垂直于抛物线的准线,垂足为C,直线
垂直于抛物线的准线,垂足为C,直线![]() 与抛物线相切于点A,交x轴于点T,给出下列命题:
与抛物线相切于点A,交x轴于点T,给出下列命题:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
其中正确的命题个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com