
【题目】已知函数![]() .
.
![]() Ⅰ
Ⅰ![]() 若函数
若函数![]() 在区间
在区间![]() 上为增函数,求a的取值范围;
上为增函数,求a的取值范围;
![]() Ⅱ
Ⅱ![]() 若对任意
若对任意![]() 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)g(x)的导数导数大于或等于0恒成立,转化成求不等式恒成立问题
(2) 求不等式恒成立问题转化成求最值问题,利用导数知识判断函数的单调性,从而求最值。
(1)由题意得g′(x)=f′(x)+a=ln x+a+1.
∵函数g(x)在区间[e2,+∞)上为增函数,∴当x∈[e2,+∞)时,g′(x)≥0,
即ln x+a+1≥0在[e2,+∞)上恒成立.∴a≥-1-ln x.
令h(x)=-ln x-1,∴a≥h(x)max,
当x∈[e2,+∞)时,ln x∈[2,+∞),
∴h(x)∈(-∞,-3],∴a≥-3,
即实数a的取值范围是[-3,+∞).
(2)∵2f(x)≥-x2+mx-3,即mx≤2xln x+x2+3,
又x>0,∴m≤![]() 在x∈(0,+∞)上恒成立.
在x∈(0,+∞)上恒成立.
记t(x)=![]() =2ln x+x+
=2ln x+x+![]() .∴m≤t(x)min.
.∴m≤t(x)min.
∵t′(x)=![]() +1-
+1-![]() =
=![]() =
=![]() ,
,
令t′(x)=0,得x=1或x=-3(舍去).
当x∈(0,1)时,t′(x)<0,函数t(x)在(0,1)上单调递减;
当x∈(1,+∞)时,t′(x)>0,函数t(x)在(1,+∞)上单调递增,∴t(x)min=t(1)=4.
∴m≤t(x)min=4,即m的最大值为4.


科目:高中数学 来源: 题型:
【题目】某超市春节大酬宾,购物满100元可参加一次抽奖活动,规则如下:顾客将一个半径适当的小球放入如图所示的容器正上方的人口处,小球在自由落下的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,顾客相应获得袋子里的奖品.已知小球每次遇到黑色障碍物时,向左向右下落的概率都为![]() .若活动当天小明在该超市购物消费108元,按照活动规则,他可参加一次抽奖,则小明获得A袋中的奖品的概率为_____.
.若活动当天小明在该超市购物消费108元,按照活动规则,他可参加一次抽奖,则小明获得A袋中的奖品的概率为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过长期观测得到:在交通繁忙的时段内,某公路汽车的车流量![]() (千辆/h)与汽车的平均速度
(千辆/h)与汽车的平均速度![]() 之间的函数关系式为:
之间的函数关系式为:![]() .
.
(1)若要求在该段时间内车流量超过2千辆![]() ,则汽车在平均速度应在什么范围内?
,则汽车在平均速度应在什么范围内?
(2)在该时段内,若规定汽车平均速度不得超过![]() ,当汽车的平均速度
,当汽车的平均速度![]() 为多少时,车流量最大?最大车流量为多少?
为多少时,车流量最大?最大车流量为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是一个“数阵”:
1 | ( ) | ( ) | ( ) | … |
| … |
( ) | 1 | ( ) | ( ) | … |
| … |
( ) | ( ) | ( ) | 1 | … |
| … |
… | … | … | … | … | … | … |
|
|
|
| … |
| … |
… | … | … | … | … | … | … |
其中每行都是公差不为0等差数列,每列都是等比数列,![]() 表示位于第i行第j列的数.
表示位于第i行第j列的数.
(1)写出![]() 的值:
的值:
(2)写出![]() 的计算公式,以及第2020个1所在“数阵”中所在的位置.
的计算公式,以及第2020个1所在“数阵”中所在的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,连结
上,连结![]() .
.
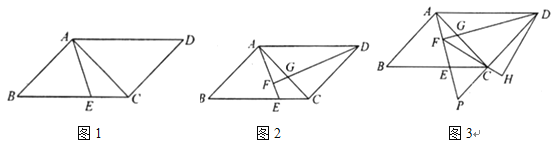
(1)若![]() ,求
,求![]() 的周长;
的周长;
(2)点![]() 是
是![]() 上一点,连结
上一点,连结![]() 交
交![]() 于点
于点![]() .
.
①如图2,若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
②如图3,连结![]() 过点
过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() 延长
延长![]() 交
交![]() 延长线于点
延长线于点![]() ,请直接写出线段
,请直接写出线段![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的离心率为2,过点
的离心率为2,过点![]() 、斜率为1的直线
、斜率为1的直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点且
两点且![]() ,
,![]() .
.
(1)求双曲线方程。
(2)设![]() 为双曲线
为双曲线![]() 右支上动点,
右支上动点,![]() 为双曲线
为双曲线![]() 的右焦点,在
的右焦点,在![]() 轴负半轴上是否存在定点
轴负半轴上是否存在定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com