
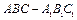 中,
中,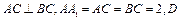 、
、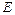 、
、 分别是
分别是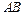 、
、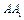 、
、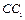 的中点,
的中点,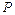 是
是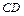 上的点.
上的点.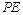 与平面
与平面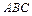 所成角的正切值的最大值;
所成角的正切值的最大值;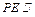 平面
平面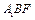 ;
;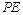 与平面
与平面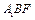 的距离.
的距离.
|

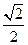
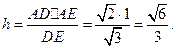
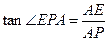
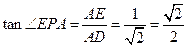
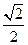 …………(4分)
…………(4分)
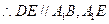
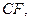
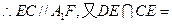
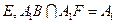 ,
,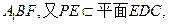
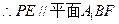 ………………………………………………………(8分)
………………………………………………………(8分)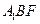 的距离等于两平行平面EDC与平面
的距离等于两平行平面EDC与平面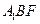 的距离,即点
的距离,即点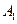 到平面EDC的距离,亦即A到平面EDC的距离.设A到平面EDC的距离为
到平面EDC的距离,亦即A到平面EDC的距离.设A到平面EDC的距离为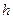 ,又
,又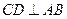 ,平面
,平面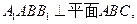 且平面
且平面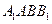 ,又
,又 ,
,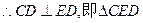 为直角三角形.
为直角三角形.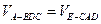 ,得
,得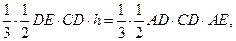
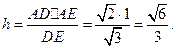 ………………………………………… (12分)
………………………………………… (12分)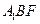 ,故平面
,故平面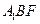 的法向量也为
的法向量也为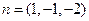 .又E到平面
.又E到平面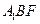 的距离,即为向量
的距离,即为向量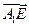 在法向量n上的投影的绝对值,
在法向量n上的投影的绝对值,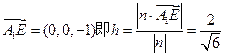 =
=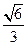


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源:不详 题型:解答题
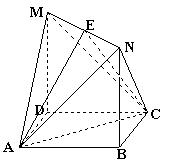
 ⊥平面AMN; (6分)
⊥平面AMN; (6分)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
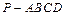 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.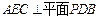 ;
; 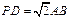 且E为PB的中点时,
且E为PB的中点时,查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
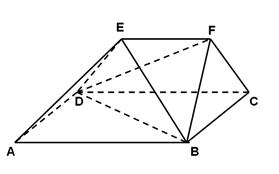
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
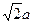 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.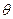 的大小.
的大小. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com