
【题目】已知函数f(x)=x2+ax,若f(f(x))的最小值与f(x)的最小值相等,则a的取值范围是 .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图①,在矩形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的中点,将三角形
的中点,将三角形![]() 沿
沿![]() 翻折到图②的位置,使得平面
翻折到图②的位置,使得平面![]()
![]() 平面
平面![]() .
.
(1)在线段![]() 上确定点
上确定点![]() ,使得
,使得![]() 平面
平面![]() ,并证明;
,并证明;
(2)求![]() 与
与![]() 所在平面构成的锐二面角的正切值.
所在平面构成的锐二面角的正切值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),锐角α的终边与单位圆O交于点P. (Ⅰ)用α的三角函数表示点P的坐标;
,0),锐角α的终边与单位圆O交于点P. (Ⅰ)用α的三角函数表示点P的坐标;
(Ⅱ)当 ![]()
![]() =﹣
=﹣ ![]() 时,求α的值;
时,求α的值;
(Ⅲ)在x轴上是否存在定点M,使得| ![]() |=
|= ![]() |
| ![]() |恒成立?若存在,求出点M的横坐标;若不存在,请说明理由.
|恒成立?若存在,求出点M的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某班学生一次英语测验的成绩分析,各分数段的分布如图(分数取整数),由此,估计这次测验的优秀率(不小于80分)为( ) 
A.92%
B.24%
C.56%
D.5.6%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证: 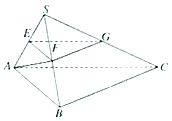
(1)平面EFG∥平面ABC;
(2)BC⊥平面SAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,若Ω是长方体ABCD﹣A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1 , 则下列结论中不正确的是( ) 
A.EH∥FG
B.四边形EFGH是矩形
C.Ω是棱柱
D.Ω是棱台
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三角形内切圆的半径是高的 ![]() ,把这个结论推广到正四面体,类似的结论正确的是( )
,把这个结论推广到正四面体,类似的结论正确的是( )
A.正四面体的内切球的半径是高的 ![]()
B.正四面体的内切球的半径是高的 ![]()
C.正四面体的内切球的半径是高的 ![]()
D.正四面体的内切球的半径是高的 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用计算机随机产生的有序二元数组(x,y)满足﹣1≤x≤1,﹣1≤y≤1.
(1)若x,y∈Z,求事件“x2+y2≤1”的概率.
(2)求事件“x2+y2>1”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com