
分析 先根据题意,以村落中心为坐标原点,向东的方向为x轴建立直角坐标系,根据两人的速度关系设其速度及各点,将实际问题转化为数学问题,利用图形中的直角三角形得到5x0=4y0,代入直线的斜率公式可得直线的斜率,再利用直线与圆相切即可的直线方程,也就得到了该问题的解.
解答  解:如图,建立平面直角坐标系,由题意可设A、B两人速度分别为3v千米/小时,
解:如图,建立平面直角坐标系,由题意可设A、B两人速度分别为3v千米/小时,
v千米/小时,再设出发x0小时,在点P改变方向,又经过y0小时,在点Q处与B相遇.
则P、Q两点坐标为(3vx0,0),(0,vx0+vy0).由|OP|2+|OQ|2=|PQ|2知,
(3vx0)2+(vx0+vy0)2=(3vy0)2,
即(x0+y0)(5x0-4y0)=0.∵x0+y0>0,∴5x0=4y0①
将①代入kPQ=-$\frac{{x}_{0}+{y}_{0}}{3{x}_{0}}$=-$\frac{3}{4}$.
又已知PQ与圆O相切,直线PQ在y轴上的截距就是两个相遇的位置.
设直线y=-$\frac{3}{4}$x+b与圆O:x2+y2=9相切,
则有$\frac{|4b|}{\sqrt{{3}^{2}+{4}^{2}}}$=3,b=$\frac{15}{4}$
答:A、B相遇点在离村中心正北$\frac{15}{4}$千米处.
点评 本题考查了圆的方程的综合应用,在这个题中注意解决实际问题的基本步骤,及题目条件的转化,体现了转化思想和数形结合思想,是个中档题.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | arctan$\frac{4}{3}$ | B. | 2arctan$\frac{4}{3}$ | C. | π-arctan$\frac{4}{3}$ | D. | π-2arctan$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
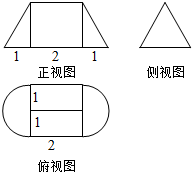 一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )| A. | 12+2$\sqrt{3}$+3π | B. | 12+3π | C. | 2$\sqrt{3}$+$\frac{{\sqrt{3}π}}{3}$ | D. | 2$\sqrt{3}$+$\sqrt{3}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com