
����Ŀ��ƹ�����������涨��һ�ֱ�����˫���ȷ���10ƽǰ��һ����������2�κԷ�����������2�Σ������ֻ�.ÿ�η���ʤ����1�֣�������0��.���ڼס��ҵı����У�ÿ�η�����1�ֵĸ���Ϊ0.6�����η����ʤ����������.�ס��ҵ�һ�ֱ����У����ȷ���.
��1����ʼ��4�η���ʱ���ס��ҵıȷ�Ϊ1��2�ĸ��ʣ�
��2��![]() ��ʾ��ʼ��4�η���ʱ�ҵĵ÷֣���
��ʾ��ʼ��4�η���ʱ�ҵĵ÷֣��� ![]() ������.
������.
���𰸡�
��1���⣺�� ![]() ��ʾ�¼�����1�κ͵ڶ��������η�����
��ʾ�¼�����1�κ͵ڶ��������η����� ![]() �֣�
�֣� ![]() ��
��
![]() ��ʾ�¼�����3�η���1�֣�
��ʾ�¼�����3�η���1�֣�
![]() ��ʾ�¼�����ʼ��4�η���ʱ�����ҵıȷ�Ϊ1��2.
��ʾ�¼�����ʼ��4�η���ʱ�����ҵıȷ�Ϊ1��2.
![]() .
.
![]()
![]()
��2���⣺ ![]() .
.
![]() �Ŀ���ȡֵΪ0��1��2��3.
�Ŀ���ȡֵΪ0��1��2��3.
![]() .
.
![]() .
.
![]() .
.
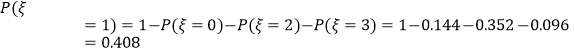 .����
.���� ![]() ��
��
![]()
![]()
��������(1)�������֪�ס��ҵıȷ�Ϊ1��2������ܵ���������֣����ݻ����¼�������¼��ĸ������ɵõ�����ʡ�(2)��������õ��� �Ŀ���ȡֵ���ö����¼��ĸ��ʹ�ʽ������Ȼ�������ѧ�����Ĺ�ʽ�����ֵ���ɡ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ex+ax����a��R������ͼ����x�ύ��A��x1 �� 0����B��x2 �� 0�����㣬��x1��x2
��1����a��ȡֵ��Χ��
��2��֤���� ![]() ����f�䣨x��Ϊf��x���ĵ�������
����f�䣨x��Ϊf��x���ĵ�������
��3�����C�ں���f��x����ͼ���ϣ��ҡ�ABCΪ�ȱ������Σ��� ![]() ����t��1����a+
����t��1����a+ ![]() ����ֵ��
����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����������ġ����ӡ����ĸ���ֱ����1��2��3��4�ĸ����֣�����һ�Ρ����ӡ�������������ֵĺ�Ϊ�����������������������ӡ����Σ�
��1����AΪ�¼��������������ӡ��ĵ�����Ϊ16�������¼�A�����ĸ��ʣ�
��2����XΪ�����������ӡ��ĵ���֮��ľ���ֵ�����������X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У�ֱ��l�IJ���������![]() ��tΪ��������������ԭ��Ϊ���㣬x���������Ϊ���ᣬ����������ϵ����֪����C�ļ����귽��Ϊ��2cos2��+��2sin2�ȩ�2��sin�ȩ�3=0��
��tΪ��������������ԭ��Ϊ���㣬x���������Ϊ���ᣬ����������ϵ����֪����C�ļ����귽��Ϊ��2cos2��+��2sin2�ȩ�2��sin�ȩ�3=0��
��1����ֱ��l�ļ����귽�̣�
��2����ֱ��l������C�ཻ��A��B���㣬��|AB|��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ ![]() �У�����C�IJ�������Ϊ
�У�����C�IJ�������Ϊ ![]() ��
�� ![]() Ϊ��������������ԭ��Ϊ���㣬
Ϊ��������������ԭ��Ϊ���㣬 ![]() ��Ǹ�����Ϊ���Ὠ��������ϵ.
��Ǹ�����Ϊ���Ὠ��������ϵ.
��1��д������C�ļ����귽�̣�
��2�����M�ļ�����Ϊ ![]() ������M��ֱ��
������M��ֱ�� ![]() ������C����A��B���㣬��
������C����A��B���㣬�� ![]() ����
���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��һ���ڽ�Ϊ
��һ���ڽ�Ϊ![]() ���������߳����ɹ���Ϊ4�ĵȲ�����,��
���������߳����ɹ���Ϊ4�ĵȲ�����,��![]() �����Ϊ�� ��
������� ��
A. 15 B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��a|��|x��4a|��a��0��������x��R������f��2x����1��f��x������ʵ��a�����ֵΪ��������
A.![]()
B.![]()
C.![]()
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��ʹ
��ʹ ![]() �����������
����������� ![]() ʹ����
ʹ���� ![]() ����㣬 �����⡰
����㣬 �����⡰ ![]() ���������⣬��ʵ��
���������⣬��ʵ�� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У�
��![]() ��
��
(1)��֤������![]() �ǵȱ�������
�ǵȱ�������
(2)������![]() ��ͨ�ʽ��
��ͨ�ʽ��
(3)��![]() ����������
����������![]() ����
����![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com