Question

一个盒子装有六张卡片，上面分别写着如下六个定义域为R的函数：f₁（x）=x，f₂（x）=x²，f₃（x）=x³，f₄（x）=sinx，f₅（x）=cosx，f₆（x）=2．
（1）现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数的概率；
（2）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取，否则继续进行，求抽取次数ξ的分布列和数学期望．

Answer 1

分析：（1）由任意两个奇函数的和为奇函数，而原来的六个函数中奇函数有三个，故可用古典概型求解；
（2）ξ可取1，2，3，4，ξ=k的含义为前k-1次取出的均为奇函数，第k次取出的是偶函数，分别求概率，列出分布列，再求期望即可．

解答：解：（1）记事件A为“任取两张卡片，将卡片上的函数相加得到的函数是奇函数”，由题意知P(A)=

C 2 3

C 2 6

=

1

5

．
（2）ξ可取1，2，3，4．P(ξ=1)=

C 1 3

C 1 6

=

1

2

，P(ξ=2)=

C 1 3

C 1 6

•

C 1 3

C 1 5

=

3

10

，P(ξ=3)=

C 1 3

C 1 6

•

C 1 2

C 1 5

•

C 1 3

C 1 4

=

3

20

，P(ξ=4)=

C 1 3

C 1 6

•

C 1 2

C 1 5

•

C 1 1

C 1 4

•

C 1 3

C 1 3

=

1

20

；
故ξ的分布列为

Eξ=1×

1

2

+2×

3

10

+3×

3

20

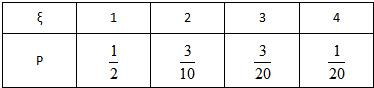+4×

1

20

=

7

4

．
答：ξ的数学期望为

7

4

．

点评：本题考查函数奇偶性的判断、排列组合、古典概型、离散型随机变量的分布列、期望等知识，及利用所学知识解决问题的能力．