
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的最小值
的最小值![]() ;
;
(2)是否存在实数![]() ,
,![]() 同时满足下列条件:①
同时满足下列条件:①![]() ;②当
;②当![]() 的定义域为
的定义域为![]() 时,其值域为
时,其值域为![]() .若存在,求出
.若存在,求出![]() ,
,![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() (a>0,b>0)的渐近线方程为y=±
(a>0,b>0)的渐近线方程为y=±![]() x,右顶点为(1,0).
x,右顶点为(1,0).
(1)求双曲线C的方程;
(2)已知直线y=x+m与双曲线C交于不同的两点A,B,且线段AB的中点为![]() ,当x0≠0时,求
,当x0≠0时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别为A1C1和BC的中点.

(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F//平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高二年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高二年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 |
| 5 |
表2:女生
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | 3 |
|
(1)由表中统计数据填写下边![]() 列联表:
列联表:
男生 | 女生 | 总计 | |||||
优秀 | |||||||
非优秀 | 总计 |
(2)试采用独立性检验进行分析,能否在犯错误的概率不超过0.1的前提下认为“测评结果优秀与性别有关”.
参考数据与公式: ,其中
,其中![]() .
.
临界值表:
| 0.1 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“工资条里显红利,个税新政人民心”,随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段,某![]() 从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁~35岁(2009年~2018年)之间各月的月平均收入
从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁~35岁(2009年~2018年)之间各月的月平均收入![]() (单位:千元)的散点图:
(单位:千元)的散点图:
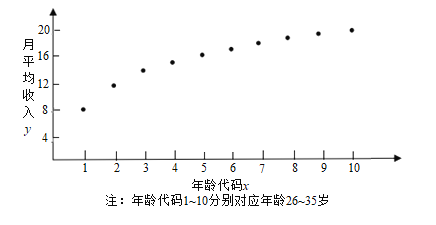
(1)由散点图知,可用回归模型![]() 拟合
拟合![]() 与
与![]() 的关系,试根据有关数据建立
的关系,试根据有关数据建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)如果该![]() 从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入为月收入,根据新旧个税政策,估计他36岁时每个月少缴交的个人所得税.
从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入为月收入,根据新旧个税政策,估计他36岁时每个月少缴交的个人所得税.
附注:
参考数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ;取
;取![]() ,
,![]()
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为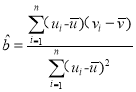 ,
,![]()
新旧个税政策下每月应纳税所得额(含税)计算方法及税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
税缴级数 | 每月应纳税所得额(含税) =收入-个税起征点 | 税率 (%) | 每月应纳税所得额(含税) =收入一个税起征点-专项附加扣除 | 税率 (%) |
1 | 不超过1500元的部分 | 3 | 不超过3000元的部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元155000元的部分 | 30 | 超过35000元至55000元的部分 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中对几何学的研究比西方早一千多年.在该书中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵;将底面为矩形,一侧棱垂直于底面的四棱锥称为阳马;将四个面均为直角三角形的四面体称为鳖臑.如图,在堑堵![]() 中,
中,![]() ,
,![]() ,鳖臑
,鳖臑![]() 的体积为2,则阳马
的体积为2,则阳马![]() 外接球表面积的最小值为__________.
外接球表面积的最小值为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产了一种新产品,在推广期邀请了100位客户试用该产品,每人一台.试用一个月之后进行回访,由客户先对产品性能作出“满意”或“不满意”的评价,再让客户决定是否购买该试用产品(不购买则可以免费退货,购买则仅需付成本价).经统计,决定退货的客户人数是总人数的一半,“对性能满意”的客户比“对性能不满意”的客户多10人,“对性能不满意”的客户中恰有![]() 选择了退货.
选择了退货.
(1)请完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“客户购买产品与对产品性能满意之间有关”.
的把握认为“客户购买产品与对产品性能满意之间有关”.
对性能满意 | 对性能不满意 | 合计 | |
购买产品 | |||
不购买产品 | |||
合计 |
(2)企业为了改进产品性能,现从“对性能不满意”的客户中按是否购买产品进行分层抽样,随机抽取6位客户进行座谈.座谈后安排了抽奖环节,共有4张奖券,奖券上分别印有200元、400元、600元和800元字样,抽到奖券可获得相应奖金.6位客户有放回的进行抽取,每人随机抽取一张奖券,求6位客户中购买产品的客户人均所得奖金不少于500元的概率.
附:![]() ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com