
【题目】设函数![]()
(Ⅰ)当![]() 时,解不等式
时,解不等式![]() ;
;
(Ⅱ)求证:![]()
【答案】(Ⅰ) ![]() (Ⅱ)详见解析
(Ⅱ)详见解析
【解析】
(Ⅰ)当a=1时,不等式f(x)≥1等价于|x+1|﹣|x﹣1|≥1,去绝对值,分段求出即可,
(Ⅱ)根据绝对值三角不等式可得f(x)![]() ,只要证明
,只要证明![]() 2即可.
2即可.
(Ⅰ)当a=1时,不等式f(x)≥1等价于|x+1|﹣|x﹣1|≥1,
当x≤﹣1时,不等式化为﹣x﹣1+x﹣1≥1,原不等式无解,
当﹣1<x<1时,不等式化为x+1+x﹣1≥1,解得![]() x<1,
x<1,
当x≥1时,不等式化为x+1﹣x+1≥1,解得x≥1,
综上所述,不等式的解集为[![]() ,+∞);
,+∞);
(Ⅱ)f(x)=|x![]() |﹣|x
|﹣|x![]() |≤|(x
|≤|(x![]() )﹣(x
)﹣(x![]() )|
)|![]() ,
,
∵a∈[0,2],
∴a+2﹣a≥2![]() ,
,
∴2[a+(2﹣a)]≥(![]() )2,
)2,
∴(![]() )2≤4,
)2≤4,
∴![]() 2,
2,
∴f(x)≤2.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,圆
,圆![]() :
: ![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() ,
, ![]() 为椭圆
为椭圆![]() 上的动点,
上的动点, ![]() ,
, ![]() 面积最大值为
面积最大值为![]() .
.
(1)求圆![]() 与椭圆
与椭圆![]() 的方程;
的方程;
(2)圆![]() 的切线
的切线![]() 交椭圆于点
交椭圆于点![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了增加某种产品的生产能力,决定改造原有生产线,需一次性投资300万元,第一年的年生产能力为300吨,随后以每年40吨的速度逐年递减,根据市场调查与预测,该产品的年销售量的频率分布直方图如图所示,该设备的使用年限为3年,该产品的销售利润为1万元![]() 吨.
吨.
![]() 1
1![]() 根据年销售量的频率分布直方图,估算年销量的平均数
根据年销售量的频率分布直方图,估算年销量的平均数![]() 同一组中的数据用该组区间的中点值作代表
同一组中的数据用该组区间的中点值作代表![]() ;
;
![]() 2
2![]() 将年销售量落入各组的频率视为概率,各组的年销售量用该组区间的中点值作年销量的估计值,并假设每年的销售量相互独立.
将年销售量落入各组的频率视为概率,各组的年销售量用该组区间的中点值作年销量的估计值,并假设每年的销售量相互独立.
![]() 根据频率分布直方图估计年销售利润不低于180万的概率和不低于220万的概率;
根据频率分布直方图估计年销售利润不低于180万的概率和不低于220万的概率;
![]() 试预测该企业3年的总净利润
试预测该企业3年的总净利润![]() 年的总净利润
年的总净利润![]() 年销售利润一投资费用
年销售利润一投资费用![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,G是线段AD延长线一点,![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,F是线段PG的中点;
,F是线段PG的中点;

![]() 求证:
求证:![]() 平面PAC;
平面PAC;
![]() 若
若![]() 时,求平面PCF与平面PAG所成二面角的余弦值.
时,求平面PCF与平面PAG所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】众所周知,大型网络游戏(下面简称网游)的运行必须依托于网络的基础上,否则会出现频繁掉线的情况,进而影响游戏的销售和推广.某网游经销商在甲地区![]() 个位置对两种类型的网络(包括“电信”和“网通”)在相同条件下进行游戏掉线测试,得到数据如下:
个位置对两种类型的网络(包括“电信”和“网通”)在相同条件下进行游戏掉线测试,得到数据如下:
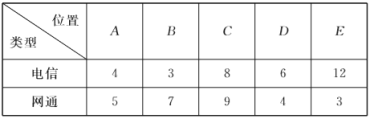
(Ⅰ)如果在测试中掉线次数超过![]() 次,则网络状况为“糟糕”,否则为“良好”,那么在犯错误的概率不超过
次,则网络状况为“糟糕”,否则为“良好”,那么在犯错误的概率不超过![]() 的前提下,能否说明网络状况与网络的类型有关?
的前提下,能否说明网络状况与网络的类型有关?
(Ⅱ)若该游戏经销商要在上述接受测试的电信的![]() 个地区中任选
个地区中任选![]() 个作为游戏推广,求
个作为游戏推广,求![]() 、
、![]() 两地区至少选到一个的概率.
两地区至少选到一个的概率.
参考公式:![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最大值为
的最大值为![]() ,其图像相邻的两条对称轴之间的距离为
,其图像相邻的两条对称轴之间的距离为![]() ,且
,且![]() 的图像关于点
的图像关于点![]() 对称,则下列结论正确的是( ).
对称,则下列结论正确的是( ).
A.函数![]() 的图像关于直线
的图像关于直线![]() 对称
对称
B.当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]()
C.若![]() ,则
,则![]() 的值为
的值为![]()
D.要得到函数![]() 的图像,只需要将
的图像,只需要将![]() 的图像向右平移
的图像向右平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年茂名市举办“好心杯”少年美术书法作品比赛,某赛区收到200件参赛作品,为了解作品质量,现从这些作品中随机抽取12件作品进行试评.成绩如下:67,82,78,86,96,81,73,84,76,59,85,93.
(1)求该样本的中位数和方差;
(2)若把成绩不低于85分(含85分)的作品认为为优秀作品,现在从这12件作品中任意抽取3件,求抽到优秀作品的件数的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com