
【题目】如图,已知直线l与抛物线y2=2x相交于A(x1 , y1),B(x2 , y2)两点,与x轴相交于点M,若y1y2=﹣4, 
(1)求:M点的坐标;
(2)求证:OA⊥OB;
(3)求△AOB的面积的最小值.
【答案】
(1)解:设M点的坐标为(t,0),直线l方程为x=my+t,
代入y2=2x得y2﹣2my﹣2t=0,①
y1、y2是此方程的两根,
∴y1y2=﹣2t=﹣4,∴t=2,即M点的坐标为(2,0)
(2)证明:∵y1y2=﹣4,
∴x1x2+y1y2= ![]() y12y22+y1y2=0,
y12y22+y1y2=0,
∴OA⊥OB;
(3)解:由方程①,y1+y2=2m,y1y2=﹣4,且|OM|=t=2,
于是S△AOB= ![]() |OM||y1﹣y2|=
|OM||y1﹣y2|= ![]() =
= ![]() ≥2,
≥2,
∴当m=0时,△AOB的面积取最小值2
【解析】(1)设M点的坐标为(t,0),直线l方程为x=my+t,代入y2=x得y2﹣2my﹣2t=0,利用韦达定理可证得M点的坐标为(2,0).(2)根据y1y2=﹣4结合向量的坐标运算得出OA⊥OB.(3)S△AOB= ![]() |OM||y1﹣y2|=
|OM||y1﹣y2|= ![]() =
= ![]() ≥2.由此能求出结果.
≥2.由此能求出结果.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥O﹣ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC= ![]() AD=2,AC平分∠BAD.
AD=2,AC平分∠BAD. 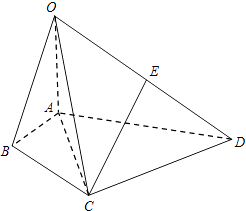
(1)求证:CE∥平面OAB;
(2)求四面体OACE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表是某校120名学生假期阅读时间(单位:小时)的频率分布表,现用分层抽样的方法从[10,15),[15,20),[20,25),[25,30)四组中抽取20名学生了解其阅读内容,那么从这四组中依次抽取的人数是( )
分组 | 频数 | 频率 |
[10,15) | 12 | 0,10 |
[15,20) | 30 | a |
[20,25) | m | 0.40 |
[25,30) | n | 0.25 |
合计 | 120 | 1.00 |
A.2,5,8,5
B.2,5,9,4
C.4,10,4,2
D.4,10,3,3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在无穷数列{an}中,a1=p是正整数,且满足 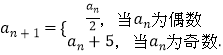 (Ⅰ)当a3=9时,给出p的值;(结论不要求证明)
(Ⅰ)当a3=9时,给出p的值;(结论不要求证明)
(Ⅱ)设p=7,数列{an}的前n项和为Sn , 求S150;
(Ⅲ)如果存在m∈N* , 使得am=1,求出符合条件的p的所有值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京是我国严重缺水的城市之一.为了倡导“节约用水,从我做起”,小明在他所在学校的2000名同学中,随机调查了40名同学家庭中一年的月均用水量(单位:吨),并将月均用水量分为6组:[2,4),[4,6),[6,8),[8,10),[10,12),[12,14]加以统计,得到如图所示的频率分布直方图. 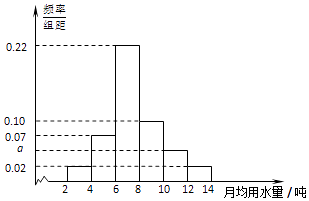
(Ⅰ)给出图中实数a的值;
(Ⅱ)根据样本数据,估计小明所在学校2000名同学家庭中,月均用水量低于8吨的约有多少户;
(Ⅲ)在月均用水量大于或等于10吨的样本数据中,小明决定随机抽取2名同学家庭进行访谈,求这2名同学中恰有1人所在家庭的月均用水量属于[10,12)组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知n次多项式 ![]() ,在求fn(x0)值的时候,不同的算法需要进行的运算次数是不同的.例如计算
,在求fn(x0)值的时候,不同的算法需要进行的运算次数是不同的.例如计算 ![]() (k=2,3,4,…,n)的值需要k﹣1次乘法运算,按这种算法进行计算f3(x0)的值共需要9次运算(6次乘法运算,3次加法运算).现按如图所示的框图进行运算,计算fn(x0)的值共需要次运算.( )
(k=2,3,4,…,n)的值需要k﹣1次乘法运算,按这种算法进行计算f3(x0)的值共需要9次运算(6次乘法运算,3次加法运算).现按如图所示的框图进行运算,计算fn(x0)的值共需要次运算.( ) 
A.2n
B.2n
C.![]()
D.n+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 ![]() 相切.
相切.
(1)求椭圆的方程;
(2)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交椭圆C于另一点E,证明直线AE与x轴相交于点Q(1,0).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为[5,15],(15,25],(25,35],(35,45],由此得到样本的重量频率分布直方图(如图), 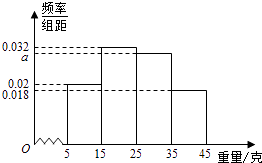
(1)求a的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
(2)从盒子中随机抽取3个小球,其中重量在[5,15]内的小球个数为X,求X的分布列和数学期望.(以直方图中的频率作为概率)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com