
【题目】过正四面体ABCD的顶点A作一个形状为等腰三角形的截面,且使截面与底面BCD所成的角为![]() ,这样的截面有( )
,这样的截面有( )
A.6个B.12个C.16个D.18个
【答案】D
【解析】
根据ABCD是正四面体和过点A的截面![]() 是等腰三角形,分
是等腰三角形,分![]() ,
,![]() ,
,![]() 讨论求解.
讨论求解.
如图,在正四面体ABCD中,因为过点A的截面![]() 是等腰三角形,
是等腰三角形,
若![]() ,则截面与底面BCD所成的角为
,则截面与底面BCD所成的角为![]() 有如下情形,
有如下情形,
如图所示:
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/2/2476065082851328/2476763358855168/EXPLANATION/c139367b863c42cd9ce450b4f4265e16.png]
在高线的两侧的截面![]() 、截面
、截面![]() 与底面BCD所成的角为
与底面BCD所成的角为![]() (
(![]() ,
,![]() 与BC平行),
与BC平行),
同理截面的一边与CD平行也有2个,与BD平行也有2个,共有6个.
若![]() ,同理也有6个;
,同理也有6个;
若![]() ,同理也有6个.
,同理也有6个.
综上所述,满足题意的截面共有18个,
故选:D.


科目:高中数学 来源: 题型:
【题目】设X是有限集,t为正整数,F是包含t个子集的子集族:F=![]() .如果F中的部分子集构成的集族S满足:对S中任意两个不相等的集合A、B,
.如果F中的部分子集构成的集族S满足:对S中任意两个不相等的集合A、B,![]() 均不成立,则称S为反链.设S1为包含集合最多的反链,S2是任意反链.证明:存在S2到S1的单射f,满足
均不成立,则称S为反链.设S1为包含集合最多的反链,S2是任意反链.证明:存在S2到S1的单射f,满足![]() 或
或![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() 过原点的直线与椭圆交于A,B两点(点A在第一象限),过点A作x轴的垂线,垂足为点
过原点的直线与椭圆交于A,B两点(点A在第一象限),过点A作x轴的垂线,垂足为点![]() ,设直线BE与椭圆的另一交点为P,连接AP得到直线l,交x轴于点M,交y轴于点N.
,设直线BE与椭圆的另一交点为P,连接AP得到直线l,交x轴于点M,交y轴于点N.
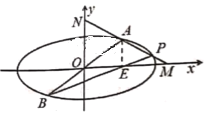
(1)若![]() ,求直线AP的斜率;
,求直线AP的斜率;
(2)记![]() 的面积分别为S1,S2,S3,求
的面积分别为S1,S2,S3,求![]() 的的最大值.
的的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() (a>b>0)的左、右焦点分别为F1,F2,过点F2的直线交椭圆于M,N两点.已知椭圆的短轴长为
(a>b>0)的左、右焦点分别为F1,F2,过点F2的直线交椭圆于M,N两点.已知椭圆的短轴长为![]() ,离心率为
,离心率为![]() .
.

(1)求椭圆的标准方程;
(2)当直线MN的斜率为![]() 时,求
时,求![]() 的值;
的值;
(3)若以MN为直径的圆与x轴相交的右交点为P(t,0),求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“牟合方盖”是我国古代数学家刘徽在研究球的体积过程中构造在一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖),其直观图如图所示,图中四边形是体现其直观性所做的辅助线,当其正视图与侧视图完全相同时,它的正视图和俯视图分别是( )


A.a,bB.a,cC.a,dD.b,d
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年新冠肺炎疫情期间,某区政府为了解本区居民对区政府防疫工作的满意度,从本区居民中随机抽取若干居民进行评分(满分
年新冠肺炎疫情期间,某区政府为了解本区居民对区政府防疫工作的满意度,从本区居民中随机抽取若干居民进行评分(满分![]() 分).根据调查数据制成如下表格和频率分布直方图.已知评分在
分).根据调查数据制成如下表格和频率分布直方图.已知评分在![]() 的居民有
的居民有![]() 人.
人.
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
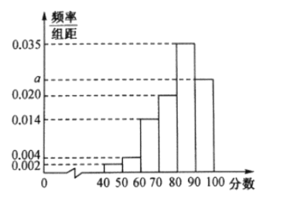
(1)求频率分布直方图中![]() 的值及所调查的总人数;
的值及所调查的总人数;
(2)定义满意度指数![]() (满意程度的平均分)/100,若
(满意程度的平均分)/100,若![]() ,则防疫工作需要进行大的调整,否则不需要大调整.根据所学知识判断该区防疫工作是否需要进行大调整?
,则防疫工作需要进行大的调整,否则不需要大调整.根据所学知识判断该区防疫工作是否需要进行大调整?
(3)为了解部分居民不满意的原因,从不满意的居民(评分在![]() 、
、![]() )中用分层抽样的方法抽取
)中用分层抽样的方法抽取![]() 名居民,倾听他们的意见,并从
名居民,倾听他们的意见,并从![]() 人中抽取
人中抽取![]() 人担任防疫工作的监督员,求这
人担任防疫工作的监督员,求这![]() 人中仅有一人对防疫工作的评分在
人中仅有一人对防疫工作的评分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx+2x﹣1.
(1)求f(x)的极值;
(2)若对任意的x>1,都有f(x)﹣k(x﹣1)>0(k∈Z)恒成立,求k的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com