
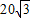 海里的C处.
海里的C处.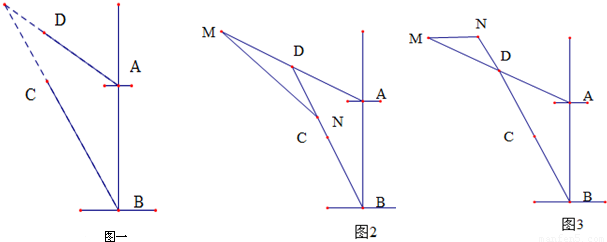
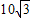 海里/小时的速度行驶,问两艘船之间的距离何时最短?
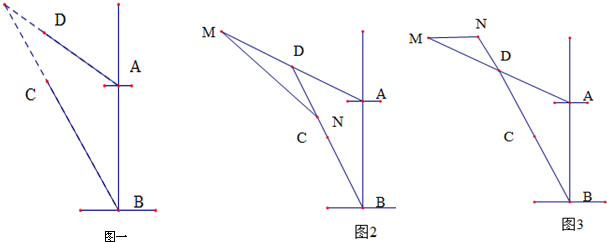
海里/小时的速度行驶,问两艘船之间的距离何时最短?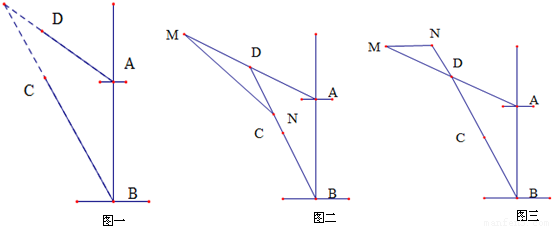 解:(Ⅰ)如图一所示,延长BC交直线AD于D1,
解:(Ⅰ)如图一所示,延长BC交直线AD于D1, =
=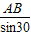 ,
,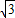 .--4分
.--4分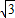 ,
,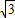 ---5分
---5分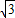 -10
-10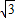 t)海里,则
t)海里,则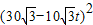 -2×10t×(30
-2×10t×(30 -10
-10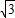 t)×cos150°=300(t2-5t+9).-----9分
t)×cos150°=300(t2-5t+9).-----9分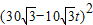 -2×10t×(10
-2×10t×(10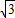 t-30
t-30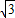 )×cos30°=300(t2-5t+9),
)×cos30°=300(t2-5t+9),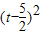 +825,
+825, ,行驶2.5小时时,两艘船之间的距离最短.--13分
,行驶2.5小时时,两艘船之间的距离最短.--13分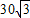 海里;(II)行驶2.5小时时,两艘船之间的距离最近.-----14分
海里;(II)行驶2.5小时时,两艘船之间的距离最近.-----14分

科目:高中数学 来源: 题型:
 如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3
如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
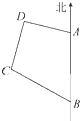
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
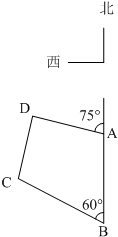
 如图,海岸线上有相距5海里的两座灯塔A,B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处.求甲、乙两艘轮船之间的距离.
如图,海岸线上有相距5海里的两座灯塔A,B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处.求甲、乙两艘轮船之间的距离.查看答案和解析>>
科目:高中数学 来源:2009年浙江省温州市瑞安中学高考数学三模试卷(理科)(解析版) 题型:解答题
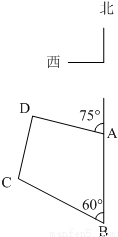 如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距
如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距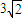 海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘船之间的距离为 海里.
海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘船之间的距离为 海里.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com