
【题目】已知常数项为![]() 的函数
的函数![]() 的导函数为
的导函数为![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(2)若![]() 在区间
在区间![]() (
(![]() 为自然对数的底数)上的最大值为
为自然对数的底数)上的最大值为![]() ,求
,求![]() 的值.
的值.
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】若椭圆的中心在原点,焦点在![]() 轴上,点
轴上,点![]() 是椭圆上的一点,
是椭圆上的一点,![]() 在
在![]() 轴上的射影恰为椭圆的左焦点,
轴上的射影恰为椭圆的左焦点,![]() 与中心
与中心![]() 的连线平行于右顶点与上顶点的连线,且左焦点与左顶点的距离等于
的连线平行于右顶点与上顶点的连线,且左焦点与左顶点的距离等于![]() ,试求椭圆的离心率及其方程.
,试求椭圆的离心率及其方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
: ![]()
![]() 的离心率为
的离心率为![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() ,点
,点![]() 在椭圆上,且异于点
在椭圆上,且异于点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 与直线
与直线![]() :
: ![]() 分别交于点
分别交于点![]() 、
、![]() ,且
,且![]() 面积的最大值为
面积的最大值为![]() .
.
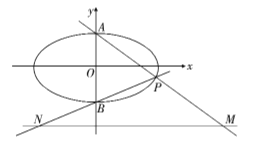
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求线段![]() 的长的最小值.
的长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高三一班元旦晚会上,有6个演唱节目,4个舞蹈节目.
(1)当4个舞蹈节目接在一起时,有多少种不同的节目安排顺序?
(2)当要求每2个舞蹈节目之间至少安排1个演唱节目时,有多少种不同的节目安排顺序?
(3)若已定好节目单,后来情况有变,需加上诗歌朗诵和快板2个节目,但不能改变原来节目的相对顺序,有多少种不同的节目演出顺序?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在侧棱垂直底面的四棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() 为
为![]() 与
与![]() 的交点.
的交点.
(I) 求线段![]() ,
,![]() 的长度;
的长度;
(II)证明:![]() 平面
平面![]() ;
;
(III)求![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com