考点:函数的周期性,函数奇偶性的性质
专题:函数的性质及应用
分析:(1)根据定义在R 上的函数f(x)满足f(x+
)+f(x)=0.可得f(x+3)+
f(x+)=0,即可得出周期性;
(2)由于f(-x)=f(3-x)=-
f(x-),f(x)=-
f(-x),而
f(x-)≠
f(-x),可得f(-x)≠f(x),
(3)函数y=f(x-
)为奇函数,可得
f(-x-)=-
f(x-),以
-x代换x可得
f(-x)+f(x)=0,即可判断出.
解答:
解:(1)∵定义在R 上的函数f(x)满足f(x+
)+f(x)=0.
∴f(x+3)+
f(x+)=0,∴f(x+3)=f(x),
∴函数f(x)的周期T=3.
(2)f(-x)=f(3-x)=-
f(x-),
而f(x)=-
f(-x),
f(x-)≠
f(-x),
∴f(-x)≠f(x),
∴函数f(x)不是偶函数.
(3)∵函数y=f(x-
)为奇函数,
∴
f(-x-)=-
f(x-),
以
-x代换x可得f(x-3)=-f
(-x)=f(x),
∴
f(-x)+f(x)=0,
∴函数f(x)的图象关于点(
,0)对称.
点评:本题考查了函数的奇偶性、周期性、对称性,考查了推理能力与计算能力,属于难题.



 名校通行证有效作业系列答案
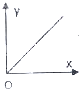
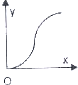
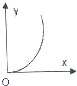
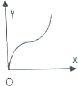
名校通行证有效作业系列答案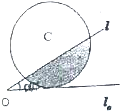 如图,已知直线l和圆C,当l从l0开始在平面上绕点O按逆时针方向匀速转动(转动角度不超过90°)时,它扫过的圆内阴影部分的面积y是时间x的函数,这个函数的图象大致是( )
如图,已知直线l和圆C,当l从l0开始在平面上绕点O按逆时针方向匀速转动(转动角度不超过90°)时,它扫过的圆内阴影部分的面积y是时间x的函数,这个函数的图象大致是( )