
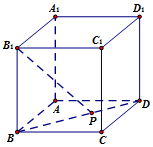
 棱长为1的正方体ABCD-A1B1C1D1中,点P在线段BD上运动.
棱长为1的正方体ABCD-A1B1C1D1中,点P在线段BD上运动.分析 (I)利用正方体与正方形的性质可得:BB1⊥AC,BP⊥AC,再利用线面垂直的判定定理即可证明结论.
(Ⅱ)以A为原点,分别以AB,AD,AA1所在直线为x,y,z轴,建立空间直角坐标系,利用向量夹角公式即可得出.
解答 (Ⅰ)证明:正方体ABCD-A1B1C1D1中,BB1⊥平面ABCD,AC?平面ABCD,则BB1⊥AC,…(2分)
正方形ABCD中,BD⊥AC,又P∈BD,则BP⊥AC,…(4分)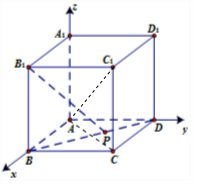
且BP∩BB1=B,∴AC⊥平面BB1P.…(5分)
(Ⅱ)以A为原点,分别以AB,AD,AA1所在直线为x,y,z轴,
建立空间直角坐标系,
则A(0,0,0),C1(1,1,1),B1(1,0,1). …(6分)
若BP=1,所以$P({1-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2},0})$,…(7分)
所以 $\overrightarrow{{B_1}P}=({-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2},-1})$,$\overrightarrow{A{C_1}}=({1,1,1})$.
则$cosα=|{cos<\overrightarrow{{B_1}P},\overrightarrow{AC}>}|=|{\frac{{\overrightarrow{{B_1}P}•\overrightarrow{AC}}}{{|{\overrightarrow{{B_1}P}}|•|{\overrightarrow{AC}}|}}}|=|{\frac{-1}{{\sqrt{2}•\sqrt{3}}}}|=\frac{{\sqrt{6}}}{6}$,
即cosθ的值为$\frac{{\sqrt{6}}}{6}$.…(12分)
点评 本题考查了正方体与正方形的性质、线面垂直的判定定理、向量夹角公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,则2x2+2x+$\frac{1}{2}$≥0 | B. | ?x0∈R,则2x02+2x0+$\frac{1}{2}$≥0 | ||
| C. | ?x0∈R,则2x02+2x0+$\frac{1}{2}$<0 | D. | ?x∈R,则2x2+2x+$\frac{1}{2}$>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | 2 | C. | $\frac{\sqrt{7}}{7}$ | D. | $\frac{\sqrt{14}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥S-ABCD中,AB∥CD,AB⊥AD,SA=AB=2CD=2,SB=2AD=2$\sqrt{2}$,平面SAB⊥平面ABCD,E为SB的中点
在四棱锥S-ABCD中,AB∥CD,AB⊥AD,SA=AB=2CD=2,SB=2AD=2$\sqrt{2}$,平面SAB⊥平面ABCD,E为SB的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com