若函数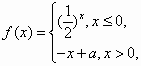
则“a＝1”是“函数y＝f(x)在R上的单调递减的”
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
科目：高中数学 来源：河北省衡水中学2012届高三第四次调研考试数学理科试题 题型：022
给出下列四个命题：
①函数f(x)＝lnx－2＋x在区间(1，e)上存在零点；
②若
(x0)＝0，则函数y＝f(x)在x＝x0处取得极值；
③若m≥－1，则函数
(x2－2x－m)的值域为R；
④“a＝1”是“函数
在定义域上是奇函数”的充分不必要条件．
其中正确的是________．
查看答案和解析>>
科目：高中数学 来源：山东省潍坊市重点中学2012届高三2月月考数学文科试题 题型：022
下列5个命题：
(1)函数y＝cosx－sinx的图象向左平移
个单位，所得函数图象关于原点对称；
(2)若命题p：“存在x∈R，x2－x－1＞0”，则命题p的否定为：“任意x∈R，x2－x－1≤0”；
(3)函数f(x)＝log
x＋x2－3的零点有2个；
(4)函数
在x＝1＋
处取最小值；
(5)已知直线x－y＋a＝0与圆x2＋y2＝1交于不同两点A、B，O为坐标原点，则“a＝1”是“向量
、
满足|＋|＝|－|”的充分不必要条件．
其中所有正确命题的序号是________．
查看答案和解析>>
科目：高中数学 来源：山东省潍坊市重点中学2012届高三2月月考数学理科试题 题型：022
下列5个命题：
(1)函数y＝cosx－sinx的图象向左平移
个单位，所得函数图象关于原点对称；
(2)若命题p：“存在x∈R，x2－x－1＞0”，则命题p的否定为：“任意x∈R，x2－x－1≤0”；
(3)函数f(x)＝log
x＋x2－3的零点有2个；
(4)函数
在x＝1＋
处取最小值；
(5)已知直线x－y＋a＝0与圆x2＋y2＝1交于不同两点A、B，O为坐标原点，则“a＝1”是“向量
、
满足|＋|＝|－|”的充分不必要条件．
其中所有正确命题的序号是________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
