
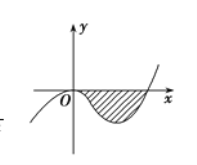
【题目】已知函数![]() 的图象如图,直线
的图象如图,直线![]() 在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为
在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若常数![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
【答案】(1)![]() ;
;
(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
试题(1)第一步:根据图形分析出两个重要的信息,过原点,并且在原点处的导数等于0,第二步,计算出图形与![]() 轴的令一个交点,求出被积区间,利用定积分求面积的公式写出定积分,最后计算出
轴的令一个交点,求出被积区间,利用定积分求面积的公式写出定积分,最后计算出![]() ;(2)根据(1)求出
;(2)根据(1)求出![]() ,第一步:求函数的导数,第二步:求函数的极值点,和判断单调区间,第三步,根据区间,并极大值
,第一步:求函数的导数,第二步:求函数的极值点,和判断单调区间,第三步,根据区间,并极大值![]() ,并求出
,并求出![]() ,因为,
,因为,![]() ,所以分
,所以分![]() 或
或![]() 两种情况进行讨论,得出最大值.
两种情况进行讨论,得出最大值.
试题解析:(1)由![]() 得
得![]() , 2分
, 2分
![]() .由
.由![]() 得
得![]() , 4分
, 4分
∴![]() ,则易知图中所围成的区域(阴影)面积为
,则易知图中所围成的区域(阴影)面积为![]() 从而得
从而得![]() ,∴
,∴![]() . 8分
. 8分
(2)由(1)知![]() .
.![]() 的取值变化情况如下:
的取值变化情况如下:
|
|
|
| 2 |
|
|
|
|
|
|
|
| 单调 | 极大值 | 单调 | 极小值 | 单调 |
又![]() ,①当
,①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() 11分
11分
综上可知:当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 12分
12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数![]() 的最小值是2;
的最小值是2;
②等差数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,
,![]() ,则当
,则当![]() 时,
时,![]() 取最大值;
取最大值;
③等比数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() ;
;
④![]() ,
,![]() 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是![]() .
.
其中所有正确命题的序号是________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某市家庭用电量的情况,该市统计局调查了200户居民去年一年的月均用电量(单位:kWh),数据从小到大排序如下:
8 18 22 31 42 48 49 50 51 56 57 57 60 61 61
61 62 62 63 63 65 66 67 69 70 70 71 72 72 74
76 77 77 78 78 80 80 82 82 82 83 84 84 88 88
89 90 91 93 93 94 95 96 96 96 97 98 98 98 99
100 100 100 101 101 101 105 106 106 106 107
107 107 107 108 108 109 109 110 110 110 111
112 113 113 114 115 116 118 120 120 120 121
123 124 127 127 127 130 130 130 131 131 132
132 132 133 133 134 134 134 135 135 135 135
136 137 137 138 139 139 140 141 142 144 146
146 147 148 149 151 152 154 156 159 160 162
163 163 164 165 167 169 170 170 172 174 174
177 178 178 180 182 182 187 189 191 191 192
194 194 200 201 201 202 203 203 206 208 212
213 214 216 223 224 237 247 250 250 251 253
254 258 260 265 274 274 283 288 289 304 319
320 324 339 462 498 530 542 626
为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯电价,使75%的居民缴费在第一档,20%的居民缴费在第二档,其余5%的居民缴费在第三档,请确定各档的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0.求分别满足下列条件的a,b的值.
(1)直线l1过点(-3,-1),并且直线l1与l2垂直;
(2)直线l1与直线l2平行,并且坐标原点到l1,l2的距离相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校的入学面试中有3道难度相当的题目,李明答对每道题目的概率都是0.6若每位面试者共有三次机会,一旦某次答对抽到的题目,则面试通过,否则就一直抽题到第3次为止,用Y表示答对题目,用N表示没有答对题目,假设对抽到的不同题目能否答对是独立的,那么
(1)请列出树状图并填写样本点,并写出样本空间;
(2)求李明第二次答题通过面试的概率;
(3)求李明最终通过面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机![]() 中的“
中的“![]() 运动”具有这样的功能,不仅可以看自己每天的运动步数,还可以看到朋友圈里好友的步数.小明的
运动”具有这样的功能,不仅可以看自己每天的运动步数,还可以看到朋友圈里好友的步数.小明的![]() 朋友圈里有大量好友参与了“
朋友圈里有大量好友参与了“![]() 运动”,他随机选取了其中30名,其中男女各15名,记录了他们某一天的走路步数,统计数据如下表所示:
运动”,他随机选取了其中30名,其中男女各15名,记录了他们某一天的走路步数,统计数据如下表所示:
|
|
|
|
|
|
男 | 0 | 2 | 4 | 7 | 2 |
女 | 1 | 3 | 7 | 3 | 1 |
(Ⅰ)以样本估计总体,视样本频率为概率,在小明![]() 朋友圈里的男性好友中任意选取3名,其中走路步数低于7500步的有
朋友圈里的男性好友中任意选取3名,其中走路步数低于7500步的有![]() 名,求
名,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)如果某人一天的走路步数超过7500步,此人将被“![]() 运动”评定为“积极型”,否则为“消极”.根据题意完成下面的
运动”评定为“积极型”,否则为“消极”.根据题意完成下面的![]() 列联表,并据此判断能否有
列联表,并据此判断能否有![]() 以上的把握认为“评定类型”与“性别”有关?
以上的把握认为“评定类型”与“性别”有关?
积极型 | 消极型 | 总计 | |
男 | |||
女 | |||
总计 |
附:![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() .以极点为原点,极轴方向为
.以极点为原点,极轴方向为![]() 轴正半轴方向,利用相同单位长度建立平面直角坐标系,直线
轴正半轴方向,利用相同单位长度建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数,
为参数,![]() 且
且![]() ).
).
(Ⅰ)写出圆![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)若直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系. 已知曲线的极坐标方程为
轴的正半轴为极轴建立极坐标系. 已知曲线的极坐标方程为![]() ,直线 的参数方程为
,直线 的参数方程为 (
(![]() 为参数).
为参数).
(I)分别求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(II)设曲线![]() 和直线
和直线![]() 相交于
相交于![]() 两点,求弦长
两点,求弦长![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com