
分析 (1)利用等差数列的通项公式及其求和公式即可得出.
(2)利用“裂项求和”方法即可得出.
解答 解:(1)设等差数列{an}的公差为d,
则$\left\{\begin{array}{l}{a_4}=7\\{S_8}=64\end{array}\right.⇒\left\{\begin{array}{l}{a_1}+3d=7\\ 8{a_1}+28d=64\end{array}\right.$,
解得a1=1,d=2,
an=1+(n-1)•2=2n-1.
(2)设数列{bn}的前n项的和为Tn.
${b_n}=\frac{1}{(2n-1)(2n+1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴${T_{100}}=\frac{1}{2}[{(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{199}-\frac{1}{201})}]$=$\frac{1}{2}(1-\frac{1}{201})=\frac{100}{201}$.
点评 本题考查了等差数列的通项公式及其求和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
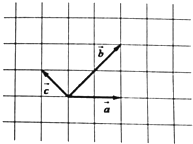 已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$在正方形网格中的位置图所示.
已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$在正方形网格中的位置图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 从某次知识竞赛中随机抽取100名考生的成绩,绘制成如图所示的频率分布直方图,分数落在区间[55,65),[65,75),[75,85)内的频率之比为4:2:1.
从某次知识竞赛中随机抽取100名考生的成绩,绘制成如图所示的频率分布直方图,分数落在区间[55,65),[65,75),[75,85)内的频率之比为4:2:1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3≤a≤6 | B. | a≥6或a≤-3 | C. | -3<a<6 | D. | a>6或a<-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ADE-BCG中,四边形ABCD是矩形,F是EG的中点,EA⊥AB,AD=AE=EF=1,平面ABGE⊥平面ABCD.
如图,三棱柱ADE-BCG中,四边形ABCD是矩形,F是EG的中点,EA⊥AB,AD=AE=EF=1,平面ABGE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC,以AB为直径的圆O与边BC,AC分别交于点D,E,且DF⊥AC于F.若CD=3,EA=$\frac{7}{5}$,则EF的长为$\frac{9}{5}$.
如图,在△ABC中,AB=AC,以AB为直径的圆O与边BC,AC分别交于点D,E,且DF⊥AC于F.若CD=3,EA=$\frac{7}{5}$,则EF的长为$\frac{9}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com