运用对数的换底公式证明
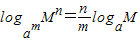
(a>0,且a≠1;M>0,m≠0).
【答案】
分析:根据对数的换底公式进行证明即可.
解答:解:等式两边同时取以a为底数的对数得
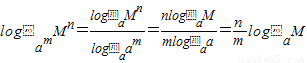
.
点评:本题主要考查对数的换底公式的应用,要求熟练掌握.
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
运用对数的换底公式证明
logamMn=logaM(a>0,且a≠1;M>0,m≠0).
查看答案和解析>>
科目:高中数学
来源:
题型:
(1)证明对数的换底公式:
logaN=(其中a>0,a≠1,N>0,c>0,c≠1).
(2)设a,b均为不等于1的正数,证明:
loganbm=logab(m∈R, n∈R, n≠0).
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
(1)证明对数的换底公式: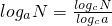 (其中a>0,a≠1,N>0,c>0,c≠1).
(其中a>0,a≠1,N>0,c>0,c≠1).
(2)设a,b均为不等于1的正数,证明: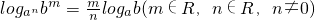 .
.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
运用对数的换底公式证明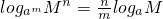 (a>0,且a≠1;M>0,m≠0).
(a>0,且a≠1;M>0,m≠0).
查看答案和解析>>

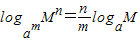 (a>0,且a≠1;M>0,m≠0).
(a>0,且a≠1;M>0,m≠0).