
【题目】如图,矩形![]() 所在平面垂直于直角梯形
所在平面垂直于直角梯形![]() 所在平面,
所在平面,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
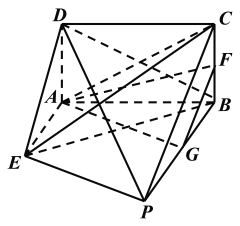
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正切值.
的正切值.
【答案】(1)见解析;(2)![]()
【解析】
(1)由几何关系可知四边形![]() 是平行四边形,则
是平行四边形,则![]() . 由线面平行的判定定理可得
. 由线面平行的判定定理可得![]() 平面
平面![]() . 由中位线的性质可知
. 由中位线的性质可知![]() ,则
,则![]() 面
面![]() 利用面面平行的判定定理即可证得平面
利用面面平行的判定定理即可证得平面![]() 平面
平面![]() .
.
(2)以![]() 为坐标原点建立空间直角坐标系,计算可得平面
为坐标原点建立空间直角坐标系,计算可得平面![]() 的一个法向量
的一个法向量![]() .而平面
.而平面![]() 的一个法向量为
的一个法向量为![]() .据此可得
.据此可得![]() ,然后结合同角三角函数基本关系求解二面角
,然后结合同角三角函数基本关系求解二面角![]() 的正切值即可.
的正切值即可.
(1)因为![]() 是
是![]() 的中点,
的中点,![]() ,所以
,所以![]() .
.
又因为![]() ,
, ![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() .
.
又因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 分别是
分别是![]() 的中点,所以
的中点,所以![]() .
.
又因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 面
面![]()
又因为![]() 平面
平面![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
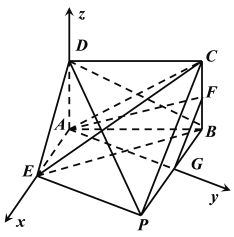
(2)以![]() 为坐标原点建立如图所示空间直角坐标系,则
为坐标原点建立如图所示空间直角坐标系,则![]() ,
,
所以![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则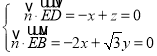 ,令
,令![]() ,得
,得![]() ,
,
所以![]() .
.
易知平面![]() 的一个法向量为
的一个法向量为![]() .
.
所以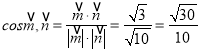 .
.
又因为二面角![]() 的平面角为锐角,所以二面角
的平面角为锐角,所以二面角![]() 的正切值
的正切值![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是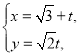 (
(![]() 为参数),曲线
为参数),曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,将曲线
,将曲线![]() 上的点向下平移1个单位,然后横坐标伸长为原来的2倍,纵坐标不变,得到曲线
上的点向下平移1个单位,然后横坐标伸长为原来的2倍,纵坐标不变,得到曲线![]() .
.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 和曲线
和曲线![]() 相交于
相交于![]() 两点,求三角形
两点,求三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学数学老师分别用两种不同教学方式对入学数学平均分和优秀率都相同的甲、乙两个高一新班(人数均为![]() 人)进行教学(两班的学生学习数学勤奋程度和自觉性一致),数学期终考试成绩茎叶图如下:
人)进行教学(两班的学生学习数学勤奋程度和自觉性一致),数学期终考试成绩茎叶图如下:
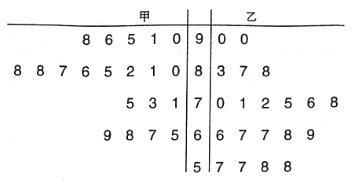
(1)现从乙班数学成绩不低于![]() 分的同学中随机抽取两名同学,求至少有一名成绩为
分的同学中随机抽取两名同学,求至少有一名成绩为![]() 分的同学被抽中的概率;
分的同学被抽中的概率;
(2)学校规定:成绩不低于![]() 分的优秀,请填写下面的
分的优秀,请填写下面的![]() 联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
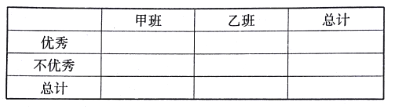
附:参考公式及数据

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场计划设计建造一条2000米长的水渠,其横断面如图所示.其中,底部是半径为1米的圆弧![]() ,上部是有一定倾角的线段
,上部是有一定倾角的线段![]() 与
与![]() ,渠深
,渠深![]() 为
为![]() 米,且圆弧
米,且圆弧![]() 的圆心为O在
的圆心为O在![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() .据测算,水渠底部曲面每平方米的造价为
.据测算,水渠底部曲面每平方米的造价为![]() 百元,上部矩形壁面每平方米的造价为1百元,其他费用忽略不计.设
百元,上部矩形壁面每平方米的造价为1百元,其他费用忽略不计.设![]() ,
,![]() .
.
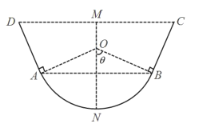
(1)试用![]() 表示水渠建造的总费用
表示水渠建造的总费用![]() (单位:百元);
(单位:百元);
(2)试确定![]() 的值,使得建造总费用最低.
的值,使得建造总费用最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2020年清明节前后3天每天下雨的概率为60%,通过模拟实验的方法来计算该地区这3天中恰好有2天下雨的概率:用随机数![]() (
(![]() ,且
,且![]() )表示是否下雨:当
)表示是否下雨:当![]() 时表示该地区下雨,当
时表示该地区下雨,当![]() 时,表示该地区不下雨,从随机数表中随机取得20组数如下
时,表示该地区不下雨,从随机数表中随机取得20组数如下
332 714 740 945 593 468 491 272 073 445
992 772 951 431 169 332 435 027 898 719
(1)求出![]() 的值,并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率;
的值,并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率;
(2)从2011年开始到2019年该地区清明节当天降雨量(单位:![]() )如下表:(其中降雨量为0表示没有下雨).
)如下表:(其中降雨量为0表示没有下雨).
时间 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
降雨量 | 29 | 28 | 26 | 27 | 25 | 23 | 24 | 22 | 21 |
经研究表明:从2011年开始至2020年, 该地区清明节有降雨的年份的降雨量![]() 与年份
与年份![]() 成线性回归,求回归直线
成线性回归,求回归直线![]() ,并计算如果该地区2020年(
,并计算如果该地区2020年(![]() )清明节有降雨的话,降雨量为多少?(精确到0.01)
)清明节有降雨的话,降雨量为多少?(精确到0.01)
参考公式: .
.
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com